Георгий  Александров

 

ИДЕАЛЬНЫЕ МАГИЧЕСКИЕ КВАДРАТЫ

 

Математика – наука удивительная; она всегда славилась красивыми открытиями, но при этом и сегодня все еще полна тайн, загадок, чудес. Находить что-то новое становится труднее и труднее, поскольку величайшие умы человечества, развивавшие науку столетиями, оставили нам в наследство вопросы, которые возможно решать только принципиально новыми методами. Так оказалось с Великой Теоремой Ферма, доказанной в 1994 году Эндрю Уальсом. Еще более впечатляющее продвижение вперед сделал в 2002-2003 годах россиянин Григорий Перельман, который убедил научный мир в справедливости знаменитой гипотезы Пуанкаре.

Помимо совершенствования логических умозаключений, набирает обороты численное моделирование. Благодаря ЭВМ мы резко продвинулись вперед в области такой древней дисциплины, как теория чисел. Уже найдены невообразимо большие числа Марсенна, получены триллионы значащих цифр числа ПИ, выявлены сотни тысяч числовых последовательностей и разложений функций в ряд.

     Особое место в математических головоломках занимают магические квадраты, рожденные в Индии свыше четырех тысяч лет назад, то есть задолго до появления шахмат.

     Магический квадрат — это квадратная таблица, заполненная n² целыми положительными числами, таким образом, что сумма в каждой строке, каждом столбце и на обеих диагоналях оказывается одинаковой.

Магические квадраты существуют для всех порядков n, за исключением n = 2, хотя случай n = 1 тривиален — квадрат состоит из одного числа. Минимальный нетривиальный случай имеет порядок 3 (заимствовано из «Википедии»).

Если магический квадрат пандиагональный (магическую константу M_n дает также и суммирование чисел в ячейках каждой диагонали, образованной при сворачивании квадрата в тор) и ассоциативный (сумма любых двух центрально противолежащих чисел постоянна и равна A_n = 1 + n²), то данный квадрат носит название “идеальный”. Магическая константа, следовательно, вычисляется так: M_n = 0,5 n A_n .

Идеальные магические квадраты (ИМК) на сегодняшний день крайне скудно изучены и целью данной книги является создание методики их построения при помощи цепей Александрова.

     Цепь (или линейно упорядоченное множество) – это множество, на котором задано отношение линейного порядка, то есть для любых двух элементов x,y указано, какой из этих элементов следует за другим. В другой терминологии: какой из этих элементов больше другого. Важнейший тип цепи – вполне упорядоченное множество (ВУМ). В последнем имеется наименьший элемент, или нуль ВУМ.

     Понятие “вполне упорядоченное множество” было введено Г.Кантором в 1883 г. Примером ВУМ служит естественным образом упорядоченное множество натуральных чисел. Согласно теореме Цермело (1904 г.), всякое непустое множество можно вполне упорядочить, а значит, образовать цепь (заимствовано из БЭС «Математика», 1998 г.).  

 

ЧТО   ИЗВЕСТНО

 

В Интернете немало примеров построенных идеальных магических квадратов. Но в основном это случайные единичные находки, обобщить которые на матрицы сколь угодно больших порядков никому не удавалось. Привожу все, что посчастливилось найти:

 

I. ИМК четного порядка:

 

http://www.magic-squares.de/eigenschaften/ultramagisch/beispiel2.html

 

Ultramagisches Quadrat 8. Ordnung

 

 

II. ИМК  нечетного порядка:

 

http://www.nefkom.net/trump/magic-squares/samples.htm

 

  

 

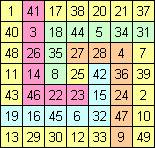
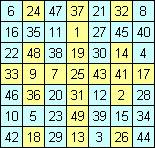
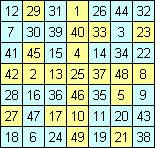
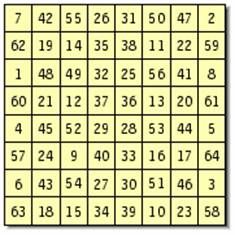
III. Решения Наталии Макаровой для ИМК нечетного порядка

 

http://www.klassikpoez.narod.ru/idealob.htm

 

1)     ИМК порядка 5

 

 

2)     ИМК порядка 7      

a) Этот квадрат она построила матричным методом, найденным по ссылке: http://www.grogono.com/magic/7x7.php

 

 

 

 

b) другой идеальный квадрат, построенный перестановкой строк из ассоциативного квадрата, построенного методом террас

 

 

 

3) ИМК порядка 9

 

 a) построен матричным методом по ссылке http://www.grogono.com/magic/7x7.php

 

 

 

 

b) ИМК получен перестановкой строк в ассоциативном квадрате, построенном на базе магического квадрата третьего порядка.

 

 

и так далее. Полностью ее исследование смотрите в ссылках «Википедии»: http://ru.wikipedia.org/wiki/Магический_квадрат

 

IV. Решения Наталии Макаровой для ИМК четно-четного порядка.

1) разработав специальную образующую таблицу, она составила 36 вариантов ИМК 8 х 8 (см. http://www.klassikpoez.narod.ru/mk/ideal8pril.htm ). Один из таких квадратов имеет вид:

 

 

2)  Два составных идеальных магических квадрата 40 х 40 – см. http://www.klassikpoez.narod.ru/ideal8.htm . Построила на основе двух ИМК: 8 х 8  и  5 х 5.

3) Там же – составной ИМК 64 х 64 .

 

3)  построила ИМК 16 х 16 путем доработки магического квадрата Франклина (http://www.klassikpoez.narod.ru/idealch.htm )

 

 

 

5) Там же, по ссылке http://www.klassikpoez.narod.ru/idealch.htm построены ИМК 24 х 24  и  32 х 32

 

6) в работе http://www.klassikpoez.narod.ru/idealch2.htm    представила ИМК 40 х 40 , скомпонованный по схеме МК  Франклина.

 

     Из разобранных примеров видно, что для построения идеальных магических квадратов изобретаются самые различные подходы, но среди них нет ни одного, который позволил бы рассчитывать ИМК любого допустимого порядка при помощи несложной программы.

 

САМЫЙ  ПРОСТОЙ  СЛУЧАЙ:

порядок  n – нечетное число, не кратное трем

 

Этот случай настолько простой, что не вызвал у меня больших проблем. Подробное изложение метода построения смотрите в  http://renuar911.narod.ru/ideal_mk.html .

 

ОБЩИЙ МЕТОД ПОСТРОЕНИЯ  ИДЕАЛЬНЫХ МАГИЧЕСКИХ КВАДРАТОВ НЕЧЕТНОГО ПОРЯДКА

 

      В  http://renuar911.narod.ru/IMSb.html впервые дан самый общий метод построения идеальных магических квадратов (ИМК) нечетного порядка  n  путем движений шахматного коня. В каждом варианте делается n  групп таких движений по n ходов. После завершения любой группы ходов производится перескок через строку вниз.

Наиболее простая схема расстановки чисел, как показали тысячи примеров компоновки ИМК, наблюдается по Рис. 21 в упомянутой выше статье. Приведу еще раз полезную структуру:

 

 

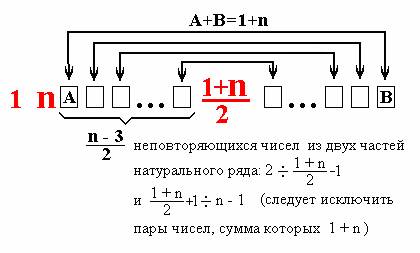
     Данная арифметическая последовательность хороша тем, что позволяет сформировать великое множество решений. Тем не менее, по рекомендации коллег-математиков, я разработал детерминированный метод построения ИМК любого нечетного порядка. Мне посчастливилось найти бесконечную последовательность чисел для той части рисунка, где показана фигурная скобка. Не вдаваясь в глубокие теоретические исследования, покажу цепочку, начинающуюся с чисел 3   6   2  . Об этой тройке смотрите упомянутую выше статью.

            Цепочка чисел Х для заполнения пространства в области фигурной скобки не допускает каких-либо вариаций и имеет ступенчатый вид:  

 

Таблица

Цепочка чисел Х в пределах фигурной скобки Рисунка

 

 

Белые ячейки – это значения n  , при которых  наблюдались проблемы при поиске ИМК. В данном случае нет никакой разницы между, например, n = 41  и  n = 51. Методика работает совершенно одинаково.

Группа 5  7  4  8  12  9 , выделенная желтым цветом, найдена простым комбинаторным анализом  всего лишь из  24-х  допустимых вариантов и оказалась единственно возможной для построения идеальных магических квадратов.  Следующая  (голубая) группа чисел – та же, что и желтая, но ее уровень на  6 единиц выше. И так далее до бесконечности. Ступеньки ряда можно продолжать строить как вручную, так и программным способом.  Столь подкупающая простота досталась мне неимоверным трудом.

            Теперь насчет значений порядка  n .  Для ячеек, закрашенных в фиолетовый цвет, нужна небольшая корректировка цепочки  X, в результате которой удастся избежать дублирования чисел. Например,  при  n = 5    решение иное: Х = 2.  Для  n = 11  вместо X = 6 нужно писать X = 4.  И так далее. Задача эта несложная и обычно сводится к замене лишь одного числа (заменяемое число показано в третьей строке Таблицы ).  Приведу пример построения цепочки для случая  n = 23. Центром цепочки будет  (1 + n)/2 = 12.  Однако, мы видим – среди значений X  в интервале n от 5 до 23 число 12 уже есть. Чтобы избежать дублирования, необходимо вместо 12 поставить число, расположенное под этой ячейкой, то есть 10.  Тогда половина цепочки станет следующей:

 

1  23  3  6  2  5  7  4  8  10  9  11  12

 

Правую ветвь достраиваем в соответствии со схемой на рисунке:

 

1  23  3  6  2  5  7  4  8  10  9  11  12  13  15  14  16  20  17  19  22  18  21

 

Как видим, в цепочке присутствуют все числа от 1 до 23 , и нигде нет повторов. Данная корректировка в программе на языке Yabasic осуществляется всего тремя командами.

Довольно интересно выглядит круговая диаграмма:

 

 

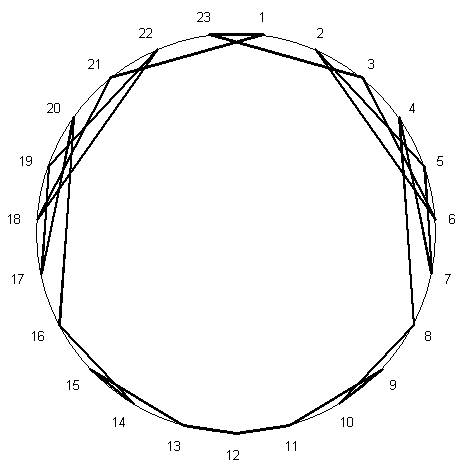
Последовательность чисел такова, что хорды почти сливаются с окружностью. Не совсем эффектно, но зато результативно.

 

ИДЕАЛЬНЫЕ МАГИЧЕСКИЕ КВАДРАТЫ
ПОРЯДКА 4k

 

     Здесь я уже шел по накатанному пути – у меня имелся метод цепей Александрова. Поэтому вполне хватило месяца работы, чтобы получить красивый результат. Он – в этих статьях:

http://renuar911.narod.ru/IMQ_8k.html  и  http://renuar911.narod.ru/IMQ_4k.html

 

     Наконец-то свершилось! Найден общий принцип построения идеальных магических квадратов 8 х 8 , 12 х 12 , 16 х 16 , 20 х 20 , то есть  4k x 4k , где k = 2, 3, 4, … . 

     Цепь Александрова строится в соответствии со следующей схемой:

 

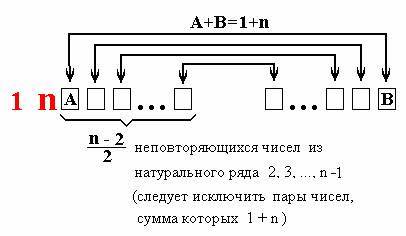
Программа на языке Yabasic позволяет быстро и надежно получать одну из многих ветвей замечательных матриц.

 

Случай 1.  n = 8k ,  k = 1, 2, 3, …

Здесь первые два числа и правая ветвь цепи Александрова компонуются из чисел p(i) по следующей схеме:

 

                                                     │

1,  n,   , , , , , , … , , │ 2,  n/2,  n/2 -2, n/2-4,  … , 4 , 3 , 5 , … , n/2-1

                                                     │

 

Квадратики заполняются  числами n + 1 - p(i)  зеркально относительно оси симметрии. 

 

В табличной форме правая ветвь выглядит так:

 

    Таблица Александрова 1

 

 

								2	4	3	n=8
						2	8	6	4	3	5	7	n=16
				2	12	10	8	6	4	3	5	7	9	11	n=24
		2	16	14	12	10	8	6	4	3	5	7	9	11	13	15	n=32
2	20	18	16	14	12	10	8	6	4	3	5	7	9	11	13	15	17	19

 

 

Случай 2.  n = 8k + 4 ,  k = 1, 2, 3, …

Цепь Александрова немного сложнее:

 

1,  n,   , , , , , , … , , │ 2, n/2+2, n/2-2, n/2-6, …, 12, n/2-3, n/2-7,…, 7, 8, 4,    3, 6, 5, 9, …, n/2-5, 10, 14,…, n/2

 

В табличной форме правая ветвь выглядит так:

 

    Таблица Александрова 2

 

 

						2	8	4	3	6	n=12
				2	12	7	8	4	3	6	5	10	n=20
		2	16	12	11	7	8	4	3	6	5	9	10		14		n=28
2	20	16	12	15	11	7	8	4	3	6	5	9	13		10		14		18			n=36

 

Самое интересное в приведенных таблицах – это наличие базовой четверки чисел: 8, 4, 3, 6 (желтая область). Коричневые ячейки образуют область, где инвариантность чисел наблюдается по вертикали. В голубых ячейках инвариантность диагональная. В зеленых – по ходу шахматного коня.

Две последние таблицы были найдены независимо друг от друга, ибо я по-разному подходил к поиску цепочек Александрова для ИМК порядка 8k  и  8k+4. Но неожиданно, уже после опубликования статей, обнаружил поразительное сходство в изменениях чисел. Скорее всего, данное обстоятельство говорит о единственности общего решения задачи построения идеальных магических квадратов четно-четного порядка методом хода шахматным конем.

Проверим последовательность 8, 4, 3, 6 на известность в «Энциклопедии числовых последовательностей:

 

     http://www.research.att.com/~njas/sequences/?q=8%2C4%2C3%2C6&language=english&go=Search

 

 

A112661       Sum of digits of previous 3 terms.         

 

     1, 1, 1, 3, 5, 9, 8, 4, 3, 6, 4, 4, 5, 4, 4, 4, 3, 2, 9, 5, 7, 3, 6, 7, 7, 2, 7, 7, 7, 3, 8, 2, 4, 5, 2, 2, 9, 4, 6, 10, 2, 9, 3, 5, 8, 7, 2, 8, 8, 9, 7, 6, 4, 8, 9, 3, 2, 5, 1, 8, 5, 5, 9, 10, 6, 7, 5, 9, 3, 8, 2, 5, 6, 4, 6, 7, 8, 3, 9, 3, 6, 9, 9, 6, 6, 3, 6, 6, 6, 9, 3, 9, 3, 6 (list; graph; listen)

Sum of digits, not iterated (i.e. not digital sum, reducing to single digit) as we twice get a term of 10 which we do not reduce to 1. This is to tribonacci (A000073) as A030132 is to Fibonacci (A000045). This has a preamble of 77 terms, then enters a cycle of length 13 (starting 3, 9, 3). The cycle length of 13 is common, as when one starts with (3, 3, 3). Note that starting with (9,9,9) gives a cycle of length 1.

     FORMULA

a(n+2) = sum of digits of (a(n) + a(n-1) + a(n-2)). a(n+2) = A007953(a(n) + a(n-1) + a(n-2)).

     CROSSREFS    

Cf. A000073, A004090, A007953, A010888, A030132.

 

Adjacent sequences: A112658 A112659 A112660 this_sequence A112662 A112663 A112664

Sequence in context: A029642 A079428 A094548 this_sequence A092996 A062949 A081500

     KEYWORD

base,easy,nonn

     AUTHOR  

Jonathan Vos Post (jvospost2(AT)yahoo.com) and Andrew Carmichael Post (andrewpost(AT)gmail.com), Dec 29 2005

 

Здесь речь идет о числах Трибоначчи, представленных однозначными цифрами. Покажем принцип построения:

 

1 + 1 + 1 = 3

1 + 1 + 3 = 5

1 + 3 + 5 = 9

3 + 5 + 9 = 17 -> 1 + 7 = 8

5 + 9 + 8 = 22 -> 2 + 2 = 4

9 + 8 + 4 = 21 -> 2 + 1 = 3

8 + 4 + 3 = 15 -> 1 + 5 = 6

И так далее…

     Что сказать по этому поводу? Можно удивляться столь неожиданному совпадению, а можно искать закономерное объяснение.

Формирование полной матрицы n x n  подробно описано в работе  http://renuar911.narod.ru/IMQ12.html

    

     На базе полученных результатов, я составил программу для построения любого допустимого идеального магического квадрата. Исключение составили следующие порядки матриц n :

3 , 4 , 4k + 2 , где k = 1, 2, 3, … .

 

rem Построение идеального магического квадрата ИМК

dim p(1000),z(1000,1000),t(1000),r(1000)

print " INPUT THE ORDER OF IMS (n = 5, 7, 8, 9, 11, 12, ... )";

input n:print

if n<5 or (n-2)/4=int((n-2)/4) then print "For n =  ";:print n;

print " decisions does not exist ":print:print:end:fi

open #1,"Ideal_n.txt","w"

rem Составление цепи Александрова

p(1)=1:p(2)=n

k=(n-4)/8

if n/2=int(n/2) then

if k=int(k) then

r1=n/2+2:p1=4*(k+1):p(r1)=2

for i=0 to k-0:p(r1+1+i)=p1-4*i:next i

p2=p1-5:r2=r1+k:p(r2)=p2

for i=0 to k-2:p(r2+i)=p2-4*i:next i

r3=r2+k-1:p(r3)=8

p(r3+1)=4:p(r3+2)=3:p(r3+3)=6

r4=r3+4:for i=0 to k-2:p(r4+i)=5+4*i:next i

r5=n:for i=0 to k-2:p(n-i)=p1-2-4*i:next i:fi

if k<>int(k) then:p(n/2+2)=2

for i=1 to n/4-1:p(n/2+2+i)=n/2-2*(i-1):next i

for j=1 to n/4-1:p(n/2+1+i+j)=3+2*(j-1):next j:fi

for i=3 to n/2+1:p(i)=n+1-p(n+3-i):next i:fi

if n/2<>int(n/2) then:n1=(n-3)/2

p(1)=1:p(2)=n:p((1+n)/2+1)=(1+n)/2:no=(n-3)/2

t(5)=3:t(7)=6:t(9)=2:if n=5 then p(3)=2:p(n)=4:fi

if n=7 then p(3)=3:p(4)=6:p(6)=2:p(n)=5:fi

if n=9 then p(3)=3:p(4)=6:p(5)=2:p(7)=8:p(8)=4:p(n)=7:fi

if n>9 then:t(11)=5:t(13)=7:t(15)=4:t(17)=8:t(19)=12

t(21)=9:s=21

for k=1 to (n+1)/2:for i=1 to 6:s=s+2:t(s)=6*k+t(9+2*i)

next i:next k

rem Блок корректировки значений t(i)

o=mod(n,12)

if o=11 then t(n-4)=t(n-4)-2:fi

if o=1 or o=7 then t(n)=t(n)-3:fi

s1=2:s0=0

for i=5 to n step 2:s1=s1+1:p(s1)=t(i):s0=s0+1:r(s0)=1+n-t(i)

next i:s1=s1+1

for i=n to 5 step -2:s1=s1+1:p(s1)=r(s0):s0=s0-1:next i:fi

s=0:s1=0:s0=0:fi:print #1

print #1,"ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = ";

print #1,n

print #1,"ЦЕПЬ АЛЕКСАНДРОВА : ";

for i=1 to n:print p(i);:print #1,p(i);:next i:print:print:print:print #1

print #1:for k=1 to n:for t=1 to n

if n/2<>int(n/2) then

if k=1 and t=1 then j=(n+1)/2:i=(n+1)/2-1:fi

if t=1 and k>1 then i=i+2:if j<0 then j=j+n:fi:if i<0 then i=i+n

fi:fi:if t>1 then i=i+1:j=j+2:fi:fi

if n/2=int(n/2) then

if k=1 and t=1 then j=1:i=1:fi

if t=1 and k>1 then i=i-1:j=j-1:if j<0 then j=j+n:fi:if i<0 then

i=i+n:fi:fi:if t>1 then i=i+1:j=j+2:fi:fi

rem приведение i и j к рамкам магического квадрата

v=i:a():i=v2:v=j:a():j=v2:z=(p(k)-1)*n+p(t):z1=int(z)

if abs(z-z1)>.9 then z=z1+1 else z=z1:fi:z(i,j)=z

next t:next k:print #1:for i=1 to n:for j=1 to n

print #1,z(i,j) using "####";

next j:print #1:print #1:next i:print #1

sub a()

v0=v/n:v1=int(v0):if v0<1 then v1=0:fi

v2=(v0-v1)*n:v3=int(v2)

if abs(v2-v3)>.9 then v2=v3+1 else z=v3:fi

if abs(v2)<.0000000001 then v2=n:fi

end sub

 

Программа составлена таким образом, что можно задаваться любым числом n (по запросу с экрана), но в тех случаях, когда ИМК невозможны, (например, при n=18) выдается сообщение:

For n = 18  decisions does not exist,  то есть:   Для n=18  решений не существует.

Рассчитаем несколько первых идеальных магических квадратов:

 

Цепь Александрова

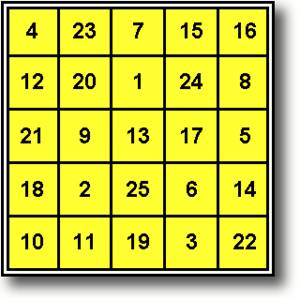
 1 5 2 3 4

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 5

 

 

 

 

 

Цепь Александрова

 1 7 3 6 4 2 5

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 7

 

 

 

 

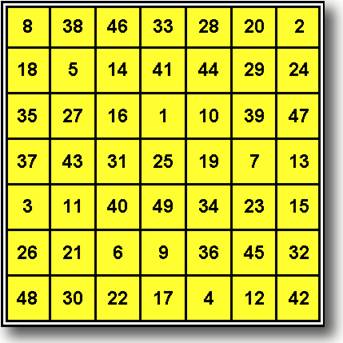
ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = 8

ЦЕПЬ АЛЕКСАНДРОВА :  1 8 6 5 7 2 4 3

 

 

 

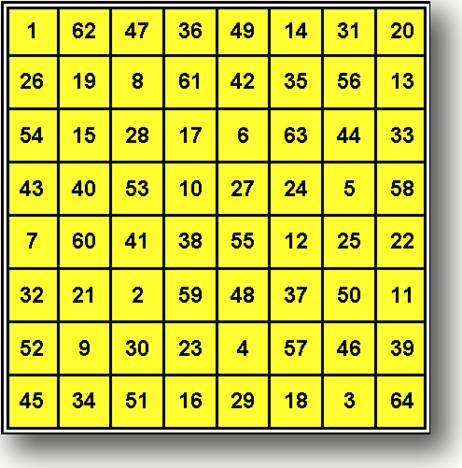
Цепь Александрова

 1 9 3 6 2 5 8 4 7

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 9

 

 

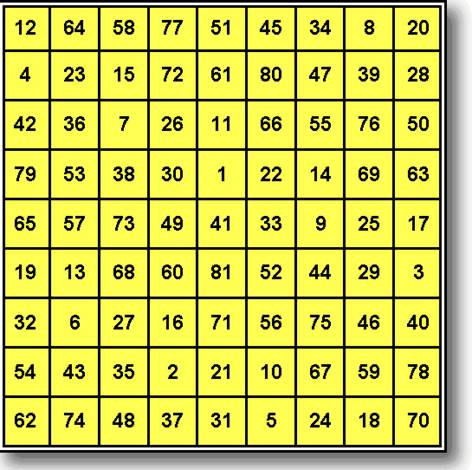
Цепь Александрова

 1 11 3 4 2 5 6 7 10 8 9

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 11

 

 

 

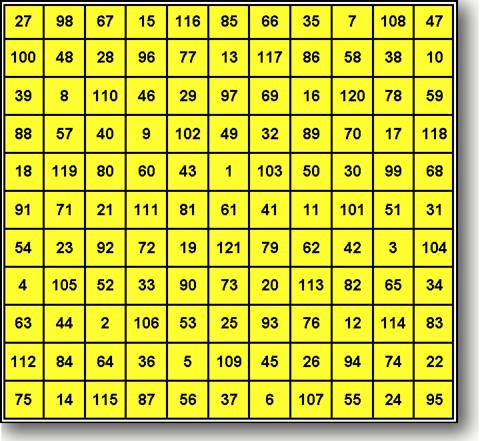
ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = 12

ЦЕПЬ АЛЕКСАНДРОВА :  1 12 7 10 9 5 11 2 8 4 3 6

 

 

 

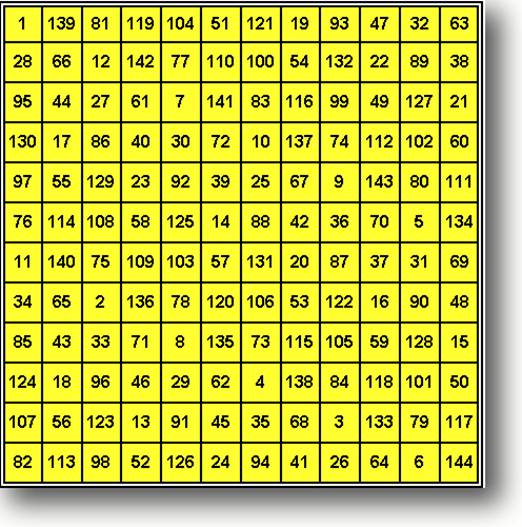
Цепь Александрова

 1 13 3 6 2 5 4 7 10 9 12 8 11

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 13

 

 

 

 

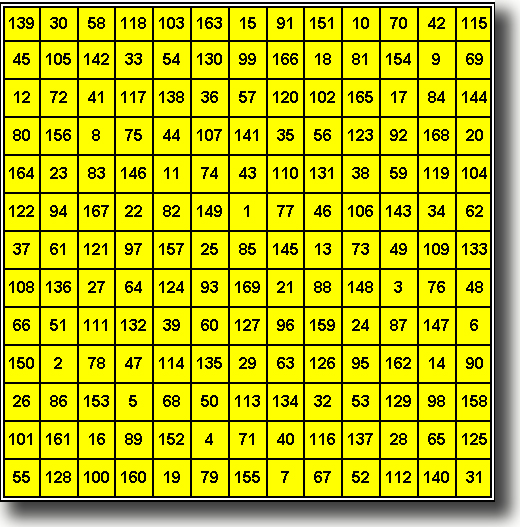
Цепь Александрова

 1 15 3 6 2 5 7 4 8 12 9 11 14 10 13

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 15

 

 

 

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = 16

ЦЕПЬ АЛЕКСАНДРОВА :  1 16 10 12 14 13 11 9 15 2 8 6 4 3 5 7

 

 

 

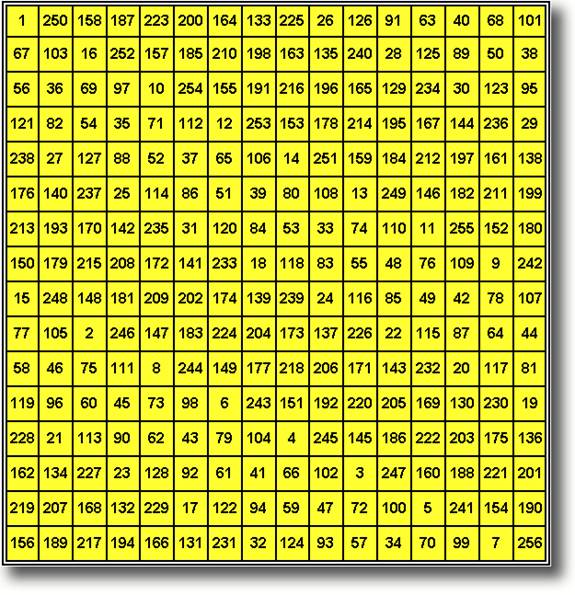
Цепь Александрова

 1 17 3 6 2 5 7 4 8 9 10 14 11 13 16 12 15

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 17

 

 

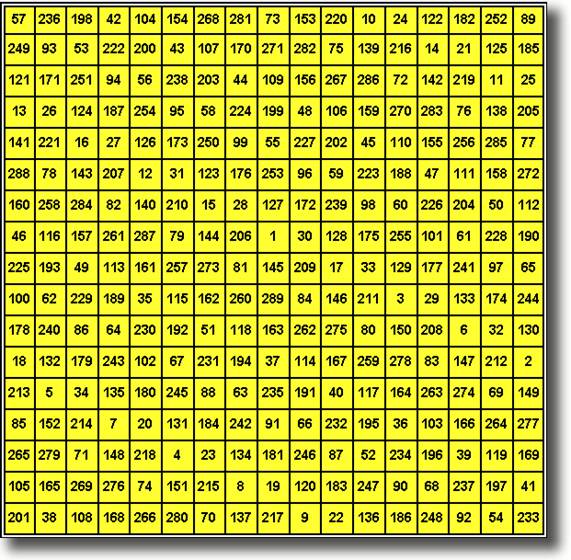
Цепь Александрова

 1 19 3 6 2 5 7 4 8 9 10 11 12 16 13 15 18 14 17

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 19

 

 

 

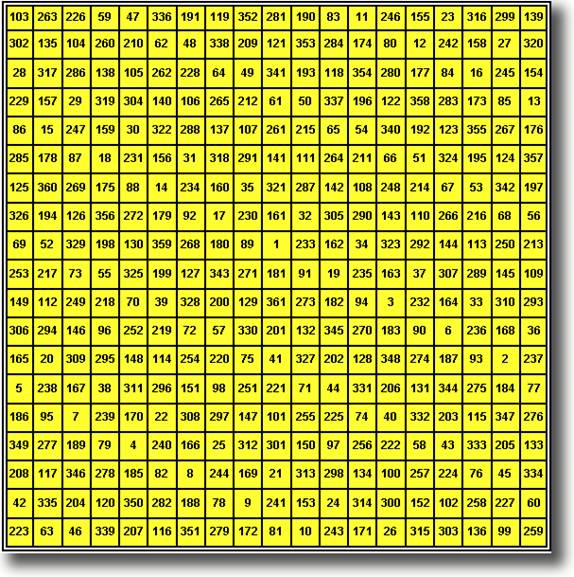
ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = 20

ЦЕПЬ АЛЕКСАНДРОВА :  1 20 11 16 15 18 17 13 14 9 19 2 12 7 8 4 3 6 5 10

 

 

 

Цепь Александрова

 1 21 3 6 2 5 7 4 8 12 9 11 13 10 14 18 15 17 20 16 19

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА 21

 

 

 

 

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = 24

ЦЕПЬ АЛЕКСАНДРОВА :  1 24 14 16 18 20 22 21 19 17 15 13 23 2 12 10 8 6 4 3 5 7 9 11

 

 

 

 

ИДЕАЛЬНЫЙ МАГИЧЕСКИЙ КВАДРАТ ПОРЯДКА n = 28

ЦЕПЬ АЛЕКСАНДРОВА :  1 28 15 19 20 24 23 26 25 21 22 18 17 13 27 2 16 12 11 7 8 4 3 6 5 9 10 14

 

 

 

 

 

 

 

РЕЗЮМЕ:

 

Я нашел метод, который по четкому сценарию находит идеальный магический квадрат заданного порядка n. Это главное. А уж имея его, можно различными перестановками чисел в ячейках (специалисты знают, какими) получать хоть миллиарды вариаций. Дело как раз заключается в том, что еще вчера никто толком не знал: существует ли вообще идеальный магический квадрат, например, 33 х 33 или 28 х 28. Находили лишь отдельные частные случаи и составные ИМК. За последние месяцы много решений нашла своими искусными преобразованиями Н.Макарова. Мне же удалось обобщить задачу для всех возможных n  методом одностороннего хода шахматным конем с привлечением математической индукции. Исключение составляют n = 3, 4, 4k+2, где k=1, 2, 3,... При этих значениях, по признанию светил теории чисел, идеальные магические квадраты вообще не могут быть скомпонованы.

 

13 мая 2008 г.