Георгий Александров
ИДЕАЛЬНЫЕ МАГИЧЕСКИЕ
КВАДРАТЫ
8 × 8 И
12 ×12
Напомню: идеальным магическим квадратом (или ИМК) называется одновременно пандиагональный и ассоциативный магический квадрат. В конце 2007 года мне удалось разработать общий метод построения ИМК нечетного порядка (см. http://renuar911.narod.ru/IMSb.html). При этом я ошибочно полагал, что ИМК четного порядка не существуют.
Однако, известный исследователь магических квадратов Н.Макарова обнаружила в Интернете ссылку, где приведен идеальный магический квадрат порядка n = 8 (см. ее статью: http://www.klassikpoez.narod.ru/ideal8.htm). Макарова тщательно проанализировала столь неожиданную находку, сделала множество преобразований и разработала различные методы построения всех четно-четных идеальных магических квадратов, за исключением случая n = 4 (2k+1), k = 1, 2, 3, … Таким образом, осталось неясным: возможно ли построить ИМК порядков 12, 20, 28, 36 , … ?
Математика, как многогранная теория, содержит в себе самые разные методы для решения одной и той же задачи. Они различаются в основном по “степени частности“. Например, метод Баше позволяет строить только магические квадраты нечетного порядка, но им невозможно воспользоваться для нахождения пандиагональных квадратов. Этого недостатка лишен мой метод цепей. С его помощью комбинаторно прокручиваются все разумные варианты и на выходе обнаруживаются: а) простые магические квадраты; б) пандиагональные квадраты и, наконец, в) жемчужины теории чисел – идеальные магические квадраты. В этом методе есть ряд сильных ограничений, благодаря которым компьютеру достаточно перелопачивать тысячи расстановок чисел вместо миллиардов, триллионов и биллионов.
Вот почему,
узнав от друзей о новой проблеме, я взял на вооружение именно свой метод цепей.
Но для начала его нужно было проверить на самом простом случае – матрице 8 х 8. Рассматривая ходы конем с
перескоками (как это мне удавалось сделать
при построении пандиагональных квадратов http://renuar911.narod.ru/MS4k_pan.html), я пришел к
выводу, что самая простая схема будет, если единицу поместить в правой нижней
ячейке, соприкасающейся с центральной точкой матрицы. При первом же ходе конем
в ячейку помещаем число n = 8.
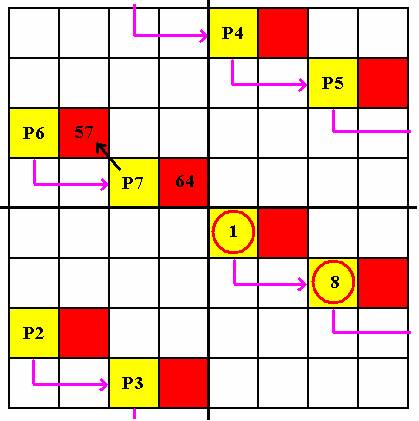
Переход с одной цепи на следующую производится по диагонали «налево-вверх» (переход с ячейки P7 на красную ячейку). В этой красной ячейке должно стоять число: ( 8 – 1 ) · n + 1 = 57. Выделенные 8 и 1 являются звеньями начальной цепи. Число 64 получается так: ( 8 – 1 ) · n + 8 . Следующая красная ячейка: ( 8 – 1 ) · n + P2 и так далее. Третья цепь начнется с числа ( P2 – 1 ) · n + 1 , затем ( P2 – 1 ) · n + 8 и так далее. Здесь мы видим, что ячейки с максимальным и минимальным числами (1 и 64) центрально- симметричны, а это есть необходимое условие построения ассоциативной матрицы.
Числа P2, …, P7 могут быть самыми различными, но на них целесообразно наложить ограничения, понять которые поможет следующая схема:
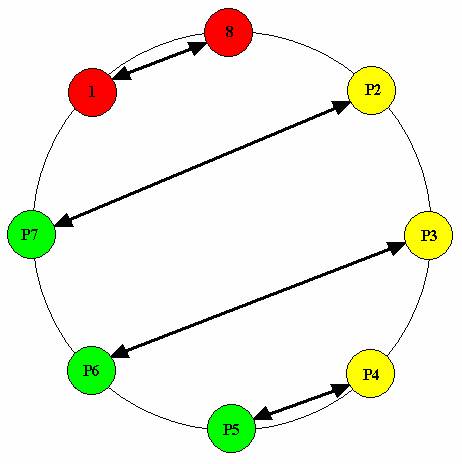
Числа в красных кружках уже нам известны как по величине, так и по местоположению в матрице. Неизвестные числа P2, …, P7 попарно зависимы. Например, P2 + P7 = n+1 , P3 + P6 = n + 1 и так далее. Тут важно учесть то обстоятельство, что среди чисел в желтых кружках не должны встретиться два таких, чтобы их сумма оказалась бы равной n+1. Общая схема составления цепей довольно простая:
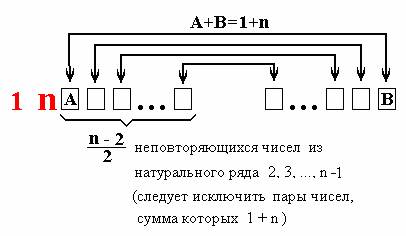
В нашем конкретном случае возможны семь комбинаций чисел P2, P3, P4 :
Файл “nam8.txt”
2 3 4
2 3 5
2 4 6
3 4 7
3 5 7
4 6 7
5 6 7
Программа “Prog8_1.yab”
rem Программа поиска цепи Александрова для ИМК8
open #1,"nam8.txt","r"
open #2,"nambers8.txt","w"
n=8:n1=1:n2=n+1
for i=1 to 7
input #1 a,b,c
t1=a:t2=b:t3=c
r=r+1
print #2,r,n1,n,t1,t2,t3,n2-t3,n2-t2,n2-t1
t1=a:t2=c:t3=b
r=r+1
print #2,r,n1,n,t1,t2,t3,n2-t3,n2-t2,n2-t1
t1=b:t2=a:t3=c
r=r+1
print #2,r,n1,n,t1,t2,t3,n2-t3,n2-t2,n2-t1
t1=b:t2=c:t3=a
r=r+1
print #2,r,n1,n,t1,t2,t3,n2-t3,n2-t2,n2-t1
t1=c:t2=a:t3=b
r=r+1
print #2,r,n1,n,t1,t2,t3,n2-t3,n2-t2,n2-t1
t1=c:t2=b:t3=a
r=r+1
print #2,r,n1,n,t1,t2,t3,n2-t3,n2-t2,n2-t1
next i
end
Выходной файл “namders8.txt”
1 1 8 2 3 4 5 6 7
2 1 8 2 4 3 6 5 7
3 1 8 3 2 4 5 7 6
4 1 8 3 4 2 7 5 6
5 1 8 4 2 3 6 7 5
6 1 8 4 3 2 7 6 5
7 1 8 2 3 5 4 6 7
8 1 8 2 5 3 6 4 7
9 1 8 3 2 5 4 7 6
10 1 8 3 5 2 7 4 6
11 1 8 5 2 3 6 7 4
12 1 8 5 3 2 7 6 4
13 1 8 2 4 6 3 5 7
14 1 8 2 6 4 5 3 7
15 1 8 4 2 6 3 7 5
16 1 8 4 6 2 7 3 5
17 1 8 6 2 4 5 7 3
18 1 8 6 4 2 7 5 3
19 1 8 3 4 7 2 5 6
20 1 8 3 7 4 5 2 6
21 1 8 4 3 7 2 6 5
22 1 8 4 7 3 6 2 5
23 1 8 7 3 4 5 6 2
24 1 8 7 4 3 6 5 2
25 1 8 3 5 7 2 4 6
26 1 8 3 7 5 4 2 6
27 1 8 5 3 7 2 6 4
28 1 8 5 7 3 6 2 4
29 1 8 7 3 5 4 6 2
30 1 8 7 5 3 6 4 2
31 1 8 4 6 7 2 3 5
32 1 8 4 7 6 3 2 5
33 1 8 6 4 7 2 5 3
34 1 8 6 7 4 5 2 3
35 1 8 7 4 6 3 5 2
36 1 8 7 6 4 5 3 2
37 1 8 5 6 7 2 3 4
38 1 8 5 7 6 3 2 4
39 1 8 6 5 7 2 4 3
40 1 8 6 7 5 4 2 3
41 1 8 7 5 6 3 4 2
42 1 8 7 6 5 4 3 2
Программа “Prog8_2.yab”
rem Построение идеального магического квадрата
dim p(1000),z(1000,1000)
n=8
open #2,"nambers8.txt","r"
open #1,"Ideal_8a.txt","w"
for q=1 to 42
print #1:print #1
input #2 y
for r1=1 to n:input
#2 p(r1):print #1,p(r1);:next r1:print #1
for k=1 to n
for t=1 to n
if k=1 and t=1 then j=n/2+1:i=n/2+1:fi
if t=1 and k>1 then i=i-1:j=j-1:if
j<0 then j=j+n:fi:if i<0
then i=i+n:fi:fi
if t>1 then i=i+1:j=j+2:fi
rem приведение i и j к рамкам магического квадрата
v=i
a()
i=v2
v=j
a()
j=v2
z=(p(k)-1)*n+p(t):z1=int(z)
if abs(z-z1)>.9 then z=z1+1 else z=z1:fi
z(i,j)=z
next t
next k
print #1
for i=1 to n
for j=1 to n
print #1,z(i,j) using
"####";
if j<>n then print #1,",";:fi
next j
print #1:print #1
next i
print #1:print #1
rem Удвоение длины МК для нахождения сумм в ломаных диагоналях
for i= 1 to n
for j=n+1 to 2*n
z(i,j)=z(i,j-n)
next j
next i
rem Построение магического квадрата удвоенной длины
for i=1 to n
for j=1 to 2*n
next j
next i
print #1, z(1,1)+z(n,n)
print "SSSSSSSSSSSSSSSSS":print
#1,"SSSSSSSSSSSSSSSSS"
rem Определение сумм по строкам, столбцам и
всем диагоналям
for i=1 to n:s=0:for j=1 to n:s=s+z(i,j)
next j:print s;:print #1,s;:next i:print:print
#1
for j=1 to n:s=0:for i=1 to n:s=s+z(j,i)
next i:print s;:print #1,s;next j:print:print
#1
Print "OOOOOOOOOO":Print #1,"OOOOOOOOOO"
for t=0 to n-1
s=0
for i=1 to n
s=s+z(i,i+t)
next i
print s;:print #1,s;
next t
print:print #1
print "WWWWWWWWW":print
#1,"WWWWWWWWW"
for t=0 to n-1
s=0
for i=n to 1 step -1
s=s+z(i,n-i+1+t)
next i
print s;:print #1,s;
next t
print:print
print #1:print #1
next q
sub a()
v0=v/n:v1=int(v0):if v0<1 then v1=0:fi
v2=(v0-v1)*n:v3=int(v2)
if abs(v2-v3)>.9 then v2=v3+1 else z=v3:fi
if abs(v2)<.0000000001 then v2=n:fi
end sub
Выходной файл "Ideal_8a.txt" ( среди 42 вариантов я выбрал только идеальные магические квадраты 8 х 8 ) :
Решение 1
1 8 4 2 6 3 7 5
46, 23, 49, 36, 6, 63, 25, 12
32, 10, 43, 21, 56, 34, 3, 61
7, 57, 28, 14, 47, 17, 52, 38
50, 35, 5, 64, 26, 11, 45, 24
41, 20, 54, 39, 1, 60, 30, 15
27, 13, 48, 18, 51, 37, 8, 58
4, 62, 31, 9, 44, 22, 55, 33
53, 40, 2, 59, 29, 16, 42, 19
Решение 2
1 8 6 2 4 5 7 3
28, 39, 49, 22, 4, 63, 41, 14
48, 10, 29, 35, 56, 18, 5, 59
7, 57, 46, 12, 31, 33, 54, 20
50, 21, 3, 64, 42, 13, 27, 40
25, 38, 52, 23, 1, 62, 44, 15
45, 11, 32, 34, 53, 19, 8, 58
6, 60, 47, 9, 30, 36, 55, 17
51, 24, 2, 61, 43, 16, 26, 37
Решение 3
1 8 4 3 7 2 6 5
55, 14, 41, 36, 7, 62, 25, 20
32, 19, 50, 13, 48, 35, 2, 61
6, 57, 28, 23, 54, 9, 44, 39
43, 34, 5, 64, 27, 18, 53, 16
49, 12, 47, 38, 1, 60, 31, 22
26, 21, 56, 11, 42, 37, 8, 59
4, 63, 30, 17, 52, 15, 46, 33
45, 40, 3, 58, 29, 24, 51, 10
Решение 4
1 8 7 3 4 5 6 2
28, 38, 41, 15, 4, 62, 49, 23
56, 19, 29, 34, 48, 11, 5, 58
6, 57, 55, 20, 30, 33, 47, 12
43, 13, 2, 64, 51, 21, 26, 40
25, 39, 44, 14, 1, 63, 52, 22
53, 18, 32, 35, 45, 10, 8, 59
7, 60, 54, 17, 31, 36, 46, 9
42, 16, 3, 61, 50, 24, 27, 37
Решение 5
1 8 6 5 7 2 4 3
55, 12, 25, 22, 7, 60, 41, 38
48, 37, 50, 11, 32, 21, 2, 59
4, 57, 46, 39, 52, 9, 30, 23
29, 18, 3, 64, 45, 34, 51, 16
49, 14, 31, 20, 1, 62, 47, 36
42, 35, 56, 13, 26, 19, 8, 61
6, 63, 44, 33, 54, 15, 28, 17
27, 24, 5, 58, 43, 40, 53, 10
Решение 6
1 8 7 5 6 3 4 2
46, 20, 25, 15, 6, 60, 49, 39
56, 37, 43, 18, 32, 13, 3, 58
4, 57, 55, 38, 44, 17, 31, 14
29, 11, 2, 64, 53, 35, 42, 24
41, 23, 30, 12, 1, 63, 54, 36
51, 34, 48, 21, 27, 10, 8, 61
7, 62, 52, 33, 47, 22, 28, 9
26, 16, 5, 59, 50, 40, 45, 19
Такую же методику применим для поиска идеальных магических квадратов 12 х 12
По программе “PROG1.yab”
rem Определение числа вариантов ИМК-12
open #1,"12-N_var.txt","w"
dim p(100),t(100),t1(100)
n=12:n1=(n-2)/2
rem Формирование чисел, участвующих в перестановках
for i=1 to n-2:p(i)=i:print p(i)+1;:next
i
print:print
rem все возможные варианты чисел в порядке возрастания
for i1=1 to n1+1
for i2=i1+1 to n1+2
for i3=i2+1 to n1+3
for i4=i3+1 to n1+4
for i5=i4+1 to n1+5
rem Блок фильтрации ненужных пар чисел, дающих в сумме n+1
k=0
t(1)=p(i1):t(2)=p(i2):t(3)=p(i3):t(4)=p(i4):t(5)=p(i5)
for i=1 to n1:for j=1 to
n1
if i<>j then:if t(i)+t(j)+2=n+1 then
k=1:fi:fi:next j:next i
if k<>1 then
for i=1 to n1:print
t(i)+1;:print #1,t(i)+1;:next
i:print:print #1:fi
next i5:next i4:next i3:next i2:next i1
ищутся возможные (n-2)/2 чисел, начиная с 2 (исключаются 1 и n ). Для n = 12 – это пять чисел. После выполнения проги в файле "12-N_var.txt" окажутся наборы:
2 3 4 5 6 -
2 3 4 5 7 -
2 3 4 6 8 -
2 3 4 7 8 - mk
2 3 5 6 9 -
2 3 5 7 9 - mk
2 3 6 8 9 - IMK !!!!
2 3 7 8 9 -
2 4 5 6 10 -
2 4 5 7 10 -
2 4 6 8 10 -
2 4 7 8 10 -
2 5 6 9 10 -
2 5 7 9 10 -
2 6 8 9 10 -
2 7 8 9 10 - IMK !!!
3 4 5 6 11 -
3 4 5 7 11 - IMK !!!
3 4 6 8 11 - IMK !!!
3 4 7 8
11 -
3 5 6 9 11 - IMK !!!
3 5 7 9
11 -
3 6 8 9
11 -
3 7 8 9
11 -
4 5 6 10
11 -
4 5 7 10
11 -
4 6 8 10
11 -
4 7 8 10
11 - mk
5 6 9 10
11 -
5 7 9 10 11 - 2 IMK !!!
6 8 9 10 11 - IMK !!!
7 8 9 10 11 -
Числа в каждой строке должны быть такими, чтобы ни одна пара не давала в сумме n+1, то есть 13.
Далее каждую пятерку чисел прогоняют при помощи “PROG2.bas” ( язык QB ):
5 OPEN "23456.txt" FOR OUTPUT AS #1
10 PRINT "Введи количество чисел"
20 INPUT "N="; n
30 DIM a(n), p(n)
32 p(1) = 2: p(2) = 3: p(3) = 6: p(4) = 8: p(5)
= 9
40 FOR i = 1 TO n
60 NEXT i
80 s = a(1)
90 FOR i = 1 TO m - 1
110 NEXT
125 IF m = a(m) THEN
140
126 ss = ss + 1
127 PRINT #1, ss;
130 FOR i = 1 TO n
133 PRINT #1, p(a(i));
134 t = t + 1: IF t = 100000 * n THEN END
135 NEXT
136 REM
137 PRINT #1,
138 GOTO 70
140 IF m = 2 THEN GOTO 170
160 GOTO 80
170 PRINT #1, ss + 1; : FOR i = 1 TO n: PRINT #1, p(i); : NEXT i
172 END
В строках с меткой 32 (я ее выделил жирным шрифтом) пишем любую строку из "12-N_var.txt" . В данном случае написан тот вариант, при котором найдено первое идеальное решение. На выходе имеем файл данных "23456.txt" :
1 3 6 8 9 2
2 6 8 9 2 3
3 8 9 2 3 6
4 9 2 3 6 8
5 3 6 8 2 9
6 6 8 2 9 3
7 8 2 9 3 6
8 2 9 3 6 8
9 9 3 6 8 2
10 6 8 2 3 9
11 8 2 3 9 6
12 2 3 9 6 8
13 3 9 6 8 2
14 9 6 8 2 3
15 8 2 3 6 9
16 2 3 6 9 8
17 3 6 9 8 2
18 6 9 8 2 3
19 9 8 2 3 6
20 3 6 2 8 9
21 6 2 8 9 3
22 2 8 9 3 6
23 8 9 3 6 2
24 9 3 6 2 8
25 6 2 8 3 9
26 2 8 3 9 6
27 8 3 9 6 2
28 3 9 6 2 8
29 9 6 2 8 3
30 2 8 3 6 9
31 8 3 6 9 2
32 3 6 9 2 8
33 6 9 2 8 3
34 9 2 8 3 6
35 8 3 6 2 9
36 3 6 2 9 8
37 6 2 9 8 3
38 2 9 8 3 6
39 9 8 3 6 2
40 6 2 3 8 9
41 2 3 8 9 6
42 3 8 9 6 2
43 8 9 6 2 3
44 9 6 2 3 8
45 2 3 8 6 9
46 3 8 6 9 2
47 8 6 9 2 3
48 6 9 2 3 8
49 9 2 3 8 6
50 3 8 6 2 9
51 8 6 2 9 3
52 6 2 9 3 8
53 2 9 3 8 6
54 9 3 8 6 2
55 8 6 2 3 9
56 6 2 3 9 8
57 2 3 9 8 6
58 3 9 8 6 2
59 9 8 6 2 3
60 3 2 6 8 9
61 2 6 8 9 3
62 6 8 9 3 2
63 8 9 3 2 6
64 9 3 2 6 8
65 2 6 8 3 9
66 6 8 3 9 2
67 8 3 9 2 6
68 3 9 2 6 8
69 9 2 6 8 3
70 6 8 3 2 9
71 8 3 2 9 6
72 3 2 9 6 8
73 2 9 6 8 3
74 9 6 8 3 2
75 8 3 2 6 9
76 3 2 6 9 8
77 2 6 9 8 3
78 6 9 8 3 2
79 9 8 3 2 6
80 2 6 3 8 9
81 6 3 8 9 2
82 3 8 9 2 6
83 8 9 2 6 3
84 9 2 6 3 8
85 6 3 8 2 9
86 3 8 2 9 6
87 8 2 9 6 3
88 2 9 6 3 8
89 9 6 3 8 2
90 3 8 2 6 9
91 8 2 6 9 3
92 2 6 9 3 8
93 6 9 3 8 2
94 9 3 8 2 6
95 8 2 6 3 9
96 2 6 3 9 8
97 6 3 9 8 2
98 3 9 8 2 6
99 9 8 2 6 3
100 6 3 2 8 9
101 3 2 8 9 6
102 2 8 9 6 3
103 8 9 6 3 2
104 9 6 3 2 8
105 3 2 8 6 9
106 2 8 6 9 3
107 8 6 9 3 2
108 6 9 3 2 8
109 9 3 2 8 6
110 2 8 6 3 9
111 8 6 3 9 2
112 6 3 9 2 8
113 3 9 2 8 6
114 9 2 8 6 3
115 8 6 3 2 9
116 6 3 2 9 8
117 3 2 9 8 6
118 2 9 8 6 3
119 9 8 6 3 2
120 2 3 6 8 9
Третий этап – составление цепей Александрова при помощи “PROG3.yab”
rem Программа поиска цепи Александрова для ИМК12
open #1,"23456.txt","r"
open #2,"23456a.txt","w"
n=12:n1=1:n2=n+1
for i=1 to 120
input #1 y,a1,a2,a3,a4,a5
r=r+1
print #2,r,n1,n,a1,a2,a3,a4,a5,n2-a5,n2-a4,n2-a3,n2-a2,n2-a1
next i
end
На выходе – файл "23456a.txt" :
1 1 12 3 6 8 9 2 11 4 5 7 10
2 1 12 6 8 9 2 3 10 11 4 5 7
3 1 12 8 9 2 3 6 7 10 11 4 5
4 1 12 9 2 3 6 8 5 7 10 11 4
5 1 12 3 6 8 2 9 4 11 5 7 10
6 1 12 6 8 2 9 3 10 4 11 5 7
7 1 12 8 2 9 3 6 7 10 4 11 5
8 1 12 2 9 3 6 8 5 7 10 4 11
9 1 12 9 3 6 8 2 11 5 7 10 4
10 1 12 6 8 2 3 9 4 10 11 5 7
11 1 12 8 2 3 9 6 7 4 10 11 5
12 1 12 2 3 9 6 8 5 7 4 10 11
13 1 12 3 9 6 8 2 11 5 7 4 10
14 1 12 9 6 8 2 3 10 11 5 7 4
15 1 12 8 2 3 6 9 4 7 10 11 5
16 1 12 2 3 6 9 8 5 4 7 10 11
17 1 12 3 6 9 8 2 11 5 4 7 10
18 1 12 6 9 8 2 3 10 11 5 4 7
19 1 12 9 8 2 3 6 7 10 11 5 4
20 1 12 3 6 2 8 9 4 5 11 7 10
21 1 12 6 2 8 9 3 10 4 5 11 7
22 1 12 2 8 9 3 6 7 10 4 5 11
23 1 12 8 9 3 6 2 11 7 10 4 5
24 1 12 9 3 6 2 8 5 11 7 10 4
25 1 12 6 2 8 3 9 4 10 5 11 7
26 1 12 2 8 3 9 6 7 4 10 5 11
27 1 12 8 3 9 6 2 11 7 4 10 5
28 1 12 3 9 6 2 8 5 11 7 4 10
29 1 12 9 6 2 8 3 10 5 11 7 4
30 1 12 2 8 3 6 9 4 7 10 5 11
31 1 12 8 3 6 9 2 11 4 7 10 5
32 1 12 3 6 9 2 8 5 11 4 7 10
33 1 12 6 9 2 8 3 10 5 11 4 7
34 1 12 9 2 8 3 6 7 10 5 11 4
35 1 12 8 3 6 2 9 4 11 7 10 5
36 1 12 3 6 2 9 8 5 4 11 7 10
37 1 12 6 2 9 8 3 10 5 4 11 7
38 1 12 2 9 8 3 6 7 10 5 4 11
39 1 12 9 8 3 6 2 11 7 10 5 4
40 1 12 6 2 3 8 9 4 5 10 11 7
41 1 12 2 3 8 9 6 7 4 5 10 11
42 1 12 3 8 9 6 2 11 7 4 5 10
43 1 12 8 9 6 2 3 10 11 7 4 5
44 1 12 9 6 2 3 8 5 10 11 7 4
45 1 12 2 3 8 6 9 4 7 5 10 11
46 1 12 3 8 6 9 2 11 4 7 5 10
47 1 12 8 6 9 2 3 10 11 4 7 5
48 1 12 6 9 2 3 8 5 10 11 4 7
49 1 12 9 2 3 8 6 7 5 10 11 4
50 1 12 3 8 6 2 9 4 11 7 5 10
51 1 12 8 6 2 9 3 10 4 11 7 5
52 1 12 6 2 9 3 8 5 10 4 11 7
53 1 12 2 9 3 8 6 7 5 10 4 11
54 1 12 9 3 8 6 2 11 7 5 10 4
55 1 12 8 6 2 3 9 4 10 11 7 5
56 1 12 6 2 3 9 8 5 4 10 11 7
57 1 12 2 3 9 8 6 7 5 4 10 11
58 1 12 3 9 8 6 2 11 7 5 4 10
59 1 12 9 8 6 2 3 10 11 7 5 4
60 1 12 3 2 6 8 9 4 5 7 11 10
61 1 12 2 6 8 9 3 10 4 5 7 11
62 1 12 6 8 9 3 2 11 10 4 5 7
63 1 12 8 9 3 2 6 7 11 10 4 5
64 1 12 9 3 2 6 8 5 7 11 10 4
65 1 12 2 6 8 3 9 4 10 5 7 11
66 1 12 6 8 3 9 2 11 4 10 5 7
67 1 12 8 3 9 2 6 7 11 4 10 5
68 1 12 3 9 2 6 8 5 7 11 4 10
69 1 12 9 2 6 8 3 10 5 7 11 4
70 1 12 6 8 3 2 9 4 11 10 5 7
71 1 12 8 3 2 9 6 7 4 11 10 5
72 1 12 3 2 9 6 8 5 7 4 11 10
73 1 12 2 9 6 8 3 10 5 7 4 11
74 1 12 9 6 8 3 2 11 10 5 7 4
75 1 12 8 3 2 6 9 4 7 11 10 5
76 1 12 3 2 6 9 8 5 4 7 11 10
77 1 12 2 6 9 8 3 10 5 4 7 11
78 1 12 6 9 8 3 2 11 10 5 4 7
79 1 12 9 8 3 2 6 7 11 10 5 4
80 1 12 2 6 3 8 9 4 5 10 7 11
81 1 12 6 3 8 9 2 11 4 5 10 7
82 1 12 3 8 9 2 6 7 11 4 5 10
83 1 12 8 9 2 6 3 10 7 11 4 5
84 1 12 9 2 6 3 8 5 10 7 11 4
85 1 12 6 3 8 2 9 4 11 5 10 7
86 1 12 3 8 2 9 6 7 4 11 5 10
87 1 12 8 2 9 6 3 10 7 4 11 5
88 1 12 2 9 6 3 8 5 10 7 4 11
89 1 12 9 6 3 8 2 11 5 10 7 4
90 1 12 3 8 2 6 9 4 7 11 5 10
91 1 12 8 2 6 9 3 10 4 7 11 5
92 1 12 2 6 9 3 8 5 10 4 7 11
93 1 12 6 9 3 8 2 11 5 10 4 7
94 1 12 9 3 8 2 6 7 11 5 10 4
95 1 12 8 2 6 3 9 4 10 7 11 5
96 1 12 2 6 3 9 8 5 4 10 7 11
97 1 12 6 3 9 8 2 11 5 4 10 7
98 1 12 3 9 8 2 6 7 11 5 4 10
99 1 12 9 8 2 6 3 10 7 11 5 4
100 1 12 6 3 2 8 9 4 5 11 10 7
101 1 12 3 2 8 9 6 7 4 5 11 10
102 1 12 2 8 9 6 3 10 7 4 5 11
103 1 12 8 9 6 3 2 11 10 7 4 5
104 1 12 9 6 3 2 8 5 11 10 7 4
105 1 12 3 2 8 6 9 4 7 5 11 10
106 1 12 2 8 6 9 3 10 4 7 5 11
107 1 12 8 6 9 3 2 11 10 4 7 5
108 1 12 6 9 3 2 8 5 11 10 4 7
109 1 12 9 3 2 8 6 7 5 11 10 4
110 1 12 2 8 6 3 9 4 10 7 5 11
111 1 12 8 6 3 9 2 11 4 10 7 5
112 1 12 6 3 9 2 8 5 11 4 10 7
113 1 12 3 9 2 8 6 7 5 11 4 10
114 1 12 9 2 8 6 3 10 7 5 11 4
115 1 12 8 6 3 2 9 4 11 10 7 5
116 1 12 6 3 2 9 8 5 4 11 10 7
117 1 12 3 2 9 8 6 7 5 4 11 10
118 1 12 2 9 8 6 3 10 7 5 4 11
119 1 12 9 8 6 3 2 11 10 7 5 4
120 1 12 2 3 6 8 9 4 5 7 10 11
И уже для каждого варианта 12 чисел строится квадрат, среди которых ищется идеальный магический. Он оказался под номером строки 115 (выделена). Программа “PROG4.yab” :
rem Построение идеального магического квадрата
dim p(1000),z(1000,1000)
n=12
open #2,"23456a.txt","r"
open #1,"Ideal_12a.txt","w"
for q=1 to 120
print #1:print #1
input #2 y
for r1=1 to n:input
#2 p(r1):print #1,p(r1);:next r1:print #1
for k=1 to n
for t=1 to n
if k=1 and t=1 then j=n/2+1:i=n/2+1:fi
if t=1 and k>1 then i=i-1:j=j-1:if
j<0 then j=j+n:fi:if i<0
then i=i+n:fi:fi
if t>1 then i=i+1:j=j+2:fi
rem приведение i и j к рамкам магического квадрата
v=i
a()
i=v2
v=j
a()
j=v2
z=(p(k)-1)*n+p(t):z1=int(z)
if abs(z-z1)>.9 then z=z1+1 else z=z1:fi
z(i,j)=z
next t
next k
print #1
for i=1 to n
for j=1 to n
print #1,z(i,j) using
"####";
if j<>n then print #1,",";:fi
next j
print #1:print #1
next i
print #1:print #1
rem Удвоение длины МК для нахождения сумм в ломаных диагоналях
for i= 1 to n
for j=n+1 to 2*n
z(i,j)=z(i,j-n)
next j
next i
rem Построение магического квадрата удвоенной длины
for i=1 to n
for j=1 to 2*n
next j
next i
print #1, z(1,1)+z(n,n)
print "SSSSSSSSSSSSSSSSS":print
#1,"SSSSSSSSSSSSSSSSS"
rem Определение
сумм по строкам,
столбцам и всем диагоналям
for i=1 to n:s=0:for j=1 to n:s=s+z(i,j)
next j:print s;:print #1,s;:next i:print:print
#1
for j=1 to n:s=0:for i=1 to n:s=s+z(j,i)
next i:print s;:print #1,s;next j:print:print
#1
Print "OOOOOOOOOO":Print #1,"OOOOOOOOOO"
for t=0 to n-1
s=0
for i=1 to n
s=s+z(i,i+t)
next i
print s;:print #1,s;
next t
print:print #1
print "WWWWWWWWW":print
#1,"WWWWWWWWW"
for t=0 to n-1
s=0
for i=n to 1 step -1
s=s+z(i,n-i+1+t)
next i
print s;:print #1,s;
next t
print:print
print #1:print #1
next q
sub a()
v0=v/n:v1=int(v0):if v0<1 then v1=0:fi
v2=(v0-v1)*n:v3=int(v2)
if abs(v2-v3)>.9 then v2=v3+1 else z=v3:fi
if abs(v2)<.0000000001 then v2=n:fi
end sub
формирует файл "Ideal_12a.txt" и среди 120 вариантов оказался искомый:
Решение 1
1 12 8 6 3 2 9 4 11 10 7 5
105, 47, 127, 109, 80,
51, 9, 143, 91,
61, 32, 15
30, 14,
100, 46, 125, 120, 78,
50, 4, 142, 89, 72
85, 68, 27,
21, 107, 43, 121, 116, 75,
57, 11, 139
10, 137, 96, 66,
26, 16, 106, 41, 132, 114,
74, 52
81, 59, 7, 133,
92, 63, 33,
23, 103, 37, 128, 111
126, 110, 76,
58, 5, 144, 90,
62, 28, 22, 101,
48
97, 44,
123, 117, 83, 55,
1, 140, 87, 69,
35, 19
34, 17,
108, 42, 122, 112, 82,
53, 12, 138, 86, 64
93, 71, 31,
13, 104, 39, 129, 119, 79,
49, 8, 135
6, 134, 88, 70,
29, 24, 102, 38, 124, 118,
77, 60
73, 56, 3, 141,
95, 67, 25,
20, 99, 45, 131, 115
130, 113, 84,
54, 2, 136, 94,
65, 36, 18,
98, 40
145
SSSSSSSSSSSSSSSSS
870 870 870 870 870
870 870 870
870 870 870
870
870 870 870 870 870
870 870 870
870 870 870
870
OOOOOOOOOO
870 870 870 870 870
870 870 870
870 870 870
870
WWWWWWWWW
870 870 870 870 870 870 870 870 870 870 870 870
Последние записи показывают, что суммы по строкам, столбцам и всем диагоналям равны магическому значению S = n (n2 + 1)/2 = 870. Число 145 – это n2 + 1 (показатель ассоциативности).
Для выявленной цепи Александрова
1 12 8 6 3 2 9 4 11 10 7 5
(она заложена в текстовом файле с именем "Model.txt" ) по программе “GRAF.yab”
open #2,"Model.txt","r"
n=12
nl=1
dim
x(100),y(100),x1(100),y1(100),p(100),b$(100)
x0=250:y0=250:r=200:r1=220:x01=240:y01=260
n0=(n+2)/2
x(n0)=x0:y(n0)=y0+r:x1(n0)=x01:y1(n0)=y01+r1
a1=2*pi/n
for i=1 to n0-1
ali=a1*(i-1)
x(i)=int(x0+r*sin(ali))
y(i)=int(y0-r*cos(ali))
x1(i)=int(x01+r1*sin(ali))
y1(i)=int(y01-r1*cos(ali))
print i,x(i),y(i)
next i
print n0,x(n0),y(n0)
for i=n0+1 to n
y(i)=y(2*n0-i)
x(i)=2*x0-x(2*n0-i)
y1(i)=y1(2*n0-i)
x1(i)=2*x01-x1(2*n0-i)
print i,x(i),y(i)
next i
for k=1 to nl
c$=str$(k,"###")
for j=1 to n
input #2 p(j)
print p(j);
next j
open window 500,500
text 30,30,c$
for w=1 to n
b$(w)=str$(w,"##")
next w
circle x0,y0,r
for f=1 to n
text x1(f),y1(f),b$(f)
next f
for i=2 to n
line x(p(i-1)),y(p(i-1)) to x(p(i)),y(p(i))
line x(p(i-1)),y(p(i-1))+1 to x(p(i)),y(p(i))+1
line x(p(i-1)),y(p(i-1))-1 to x(p(i)),y(p(i))-1
line x(p(i-1))+1,y(p(i-1)) to x(p(i))+1,y(p(i))
line x(p(i-1))-1,y(p(i-1)) to x(p(i))+1,y(p(i))
next i
line x(p(n)),y(p(n)) to x(p(1)),y(p(1))
line x(p(n)),y(p(n))+1 to x(p(1)),y(p(1))+1
line x(p(n)),y(p(n))-1 to x(p(1)),y(p(1))-1
line x(p(n))+1,y(p(n)) to x(p(1))+1,y(p(1))
line x(p(n))-1,y(p(n)) to x(p(1))-1,y(p(1))
input a
close window
next k
находим круговую схему цепи:
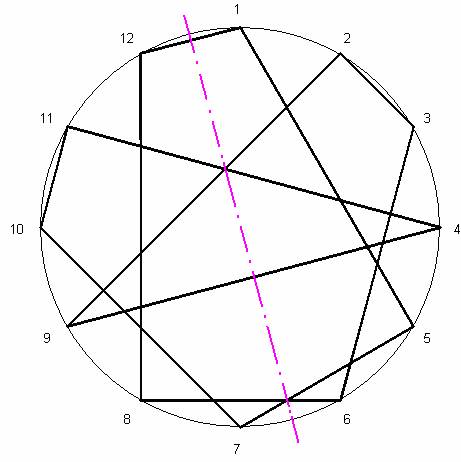
Она симметрична относительно оси, проведенной между числами 1 и 12; 6 и 7.
Идеальный магический квадрат 12 х 12 с выделенными нечетными числами :
|
105 |
47 |
127 |
109 |
80 |
51 |
9 |
143 |
91 |
61 |
32 |
15 |
|
30 |
14 |
100 |
46 |
125 |
120 |
78 |
50 |
4 |
142 |
89 |
72 |
|
85 |
68 |
27 |
21 |
107 |
43 |
121 |
116 |
75 |
57 |
11 |
139 |
|
10 |
137 |
96 |
66 |
26 |
16 |
106 |
41 |
132 |
114 |
74 |
52 |
|
81 |
59 |
7 |
133 |
92 |
63 |
33 |
23 |
103 |
37 |
128 |
111 |
|
126 |
110 |
76 |
58 |
5 |
144 |
90 |
62 |
28 |
22 |
101 |
48 |
|
97 |
44 |
123 |
117 |
83 |
55 |
1 |
140 |
87 |
69 |
35 |
19 |
|
34 |
17 |
108 |
42 |
122 |
112 |
82 |
53 |
12 |
138 |
86 |
64 |
|
93 |
71 |
31 |
13 |
104 |
39 |
129 |
119 |
79 |
49 |
8 |
135 |
|
6 |
134 |
88 |
70 |
29 |
24 |
102 |
38 |
124 |
118 |
77 |
60 |
|
73 |
56 |
3 |
141 |
95 |
67 |
25 |
20 |
99 |
45 |
131 |
115 |
|
130 |
113 |
84 |
54 |
2 |
136 |
94 |
65 |
36 |
18 |
98 |
40 |
Таким же приемом было найдено еще 7 решений:
Решение 2
1 12 8 10 7 2 9 4 11 6
3 5
105, 47, 123, 61,
32, 55, 9, 143,
87, 109, 80, 19
82, 14, 100, 42, 125,
72, 34, 50,
4, 138, 89, 120
85, 116, 79, 21, 107,
39, 121, 68, 31,
57, 11, 135
6, 137, 96, 118, 74, 16,
102, 41, 132, 70,
26, 52
33, 59, 3, 133,
92, 115, 81, 23,
99, 37, 128, 67
130, 62, 28,
54, 5, 144, 94, 110,
76, 18, 101, 48
97, 44, 127, 69,
35, 51, 1, 140,
91, 117, 83, 15
78, 17, 108, 46, 122,
64, 30, 53,
12, 142, 86, 112
93, 119, 75, 13, 104,
43, 129, 71, 27,
49, 8, 139
10, 134, 88, 114, 77,
24, 106, 38, 124, 66,
29, 60
25, 56, 7, 141,
95, 111, 73, 20, 103,
45, 131, 63
126, 65, 36,
58, 2, 136, 90, 113,
84, 22, 98, 40
Решение 3
1 12 7 4 3 5 11 2 8 10 9 6
131, 20, 93, 109, 103, 63, 11, 140, 81, 37, 31, 51
28, 53, 122, 22, 90, 120, 100, 65, 2, 142, 78, 48
73, 43, 27, 59, 128, 21, 85, 115, 99, 71, 8, 141
10, 138, 84, 40, 29, 50, 130, 18, 96, 112, 101, 62
107, 68, 9, 133, 79, 39, 35, 56, 129, 13, 91, 111
88, 113, 98, 70, 6, 144, 76, 41, 26, 58, 126, 24
121, 19, 87, 119, 104, 69, 1, 139, 75, 47, 32, 57
34, 54, 132, 16, 89, 110, 106, 66, 12, 136, 77, 38
83, 44, 33, 49, 127, 15, 95, 116, 105, 61, 7, 135
4, 137, 74, 46, 30, 60, 124, 17, 86, 118, 102, 72
97, 67, 3, 143, 80, 45, 25, 55, 123, 23, 92, 117
94, 114, 108, 64, 5, 134, 82, 42, 36, 52, 125, 14
Решение 4
1 12 8 4 3 6 11 2 7 10 9 5
131, 19, 81, 109, 104, 51, 11, 139, 93, 37, 32, 63
28, 66, 122, 22, 77, 120, 100, 54, 2, 142, 89, 48
85, 44, 27, 71, 127, 21, 73, 116, 99, 59, 7, 141
10, 137, 96, 40, 30, 62, 130, 17, 84, 112, 102, 50
107, 55, 9, 133, 92, 39, 35, 67, 129, 13, 80, 111
76, 114, 98, 58, 5, 144, 88, 42, 26, 70, 125, 24
121, 20, 75, 119, 103, 57, 1, 140, 87, 47, 31, 69
34, 65, 132, 16, 78, 110, 106, 53, 12, 136, 90, 38
95, 43, 33, 61, 128, 15, 83, 115, 105, 49, 8, 135
4, 138, 86, 46, 29, 72, 124, 18, 74, 118, 101, 60
97, 56, 3, 143, 91, 45, 25, 68, 123, 23, 79, 117
82, 113, 108, 52, 6, 134, 94, 41, 36, 64, 126, 14
Решение 5
1 12 11 6 3 5 9 4 8 10 7 2
105, 44, 91, 109, 83, 15, 9, 140, 127, 61, 35, 51
30, 53, 100, 46, 86, 120, 78, 17, 4, 142, 122, 72
121, 71, 27, 57, 104, 43, 85, 119, 75, 21, 8, 139
10, 134, 132, 66, 29, 52, 106, 38, 96, 114, 77, 16
81, 20, 7, 133, 131, 63, 33, 56, 103, 37, 95, 111
90, 113, 76, 22, 2, 144, 126, 65, 28, 58, 98, 48
97, 47, 87, 117, 80, 19, 1, 143, 123, 69, 32, 55
34, 50, 108, 42, 89, 112, 82, 14, 12, 138, 125, 64
129, 68, 31, 49, 107, 39, 93, 116, 79, 13, 11, 135
6, 137, 124, 70, 26, 60, 102, 41, 88, 118, 74, 24
73, 23, 3, 141, 128, 67, 25, 59, 99, 45, 92, 115
94, 110, 84, 18, 5, 136, 130, 62, 36, 54, 101, 40
Решение 6
1 12 7 10 9 5 11 2 8 4
3 6
131, 20, 87,
37, 31, 69,
11, 140, 75, 109, 103, 57
106, 53, 122, 16,
90, 48, 34,
65, 2, 136, 78, 120
73,
115, 105, 59,
128, 15,
85, 43, 33,
71, 8, 135
4, 138, 84, 118, 101, 50, 124,
18, 96, 46,
29, 62
35, 68, 3, 133,
79, 117, 107, 56, 123, 13,
91, 45
94, 41, 26,
64, 6, 144, 82, 113,
98, 52, 126, 24
121, 19, 93,
47, 32, 63,
1, 139, 81, 119, 104, 51
100, 54, 132, 22,
89, 38, 28,
66, 12, 142, 77, 110
83, 116, 99, 49, 127,
21, 95, 44,
27, 61, 7, 141
10, 137, 74, 112, 102, 60, 130,
17, 86, 40,
30, 72
25, 67, 9, 143,
80, 111, 97, 55, 129,
23, 92, 39
88, 42, 36,
70, 5, 134, 76, 114, 108,
58, 125, 14
Решение 7
1 12 11 10 7 5 9 4 8 6
3 2
105, 44, 87,
61, 35, 19,
9, 140, 123, 109, 83, 55
82, 53, 100, 42,
86, 72, 34,
17, 4, 138, 122, 120
121, 119, 79, 57, 104,
39, 85, 71,
31, 21, 8, 135
6,
134, 132, 118, 77, 52, 102,
38, 96, 70,
29, 16
33, 20, 3, 133, 131, 115, 81,
56, 99, 37,
95, 67
94, 65, 28,
18, 2, 144, 130, 113, 76,
54, 98, 48
97, 47, 91,
69, 32, 15,
1, 143, 127, 117, 80, 51
78, 50, 108, 46,
89, 64, 30,
14, 12, 142, 125, 112
129, 116, 75, 49, 107,
43, 93, 68,
27, 13, 11, 139
10,
137, 124, 114, 74, 60, 106,
41, 88, 66,
26, 24
25, 23, 7, 141, 128, 111, 73,
59, 103, 45, 92, 63
90, 62, 36,
22, 5, 136, 126, 110, 84,
58, 101, 40
Решение 8
1 12 8 10 9 6 11 2 7 4
3 5
131, 19, 75,
37, 32, 57,
11, 139, 87, 109, 104, 69
106, 66, 122, 16,
77, 48, 34,
54, 2, 136, 89, 120
85,
116, 105, 71,
127, 15,
73, 44, 33,
59, 7, 135
4, 137, 96, 118, 102, 62, 124,
17, 84, 46,
30, 50
35, 55, 3, 133,
92, 117, 107, 67, 123, 13,
80, 45
82, 42, 26,
52, 5, 144, 94, 114,
98, 64, 125, 24
121, 20, 81,
47, 31, 51,
1, 140, 93, 119, 103, 63
100, 65, 132, 22,
78, 38, 28,
53, 12, 142, 90, 110
95, 115, 99, 61, 128,
21, 83, 43,
27, 49, 8, 141
10, 138, 86, 112, 101, 72, 130,
18, 74, 40,
29, 60
25, 56, 9, 143,
91, 111, 97, 68, 129,
23, 79, 39
76, 41, 36,
58, 6, 134, 88, 113, 108,
70, 126, 14
Я показал свой метод, доказал его работоспособность и твердо знаю – он годится для построения всех ИМК порядка 4k при k>1. Чтобы найти ИМК20 потребуется значительно больший объем вычислений чем для решенных выше. Ручным способом тут уже не обойтись, и придется создавать специальную программу автоматизированного поиска идеальных решений. На это уйдет максимум неделя. Здесь же я описал основной принцип и сделал это, в первую очередь, для самого себя - чтобы не забыть алгоритмы и ход рассуждений. Но совершенно очевидно: ходом шахматного коня находятся уже две большие группы идеальных магических квадратов – нечетного порядка и порядка двойной четности.
Сидней
7 мая 2008
(день восхождения на престол
Дмитрия Медведева)