Георгий Александров

Георгий Александров

Идеальные магические квадраты.

Общий метод построения

Безупречен метод, дающий идеальные решения

А.Колмогоров

Даже очень сложный метод, но единственный, что дает решение, я назову прекрасным.

К.Гаусс

Халат можно сшить из отдельных лоскутов, но лучше - из цельной, красивой ткани.

Восточная мудрость

Потребность критиковать ведет к потере способностей.

Спиноза

Идеальным магическим квадратом (ИМК) порядка n принято считать пандиагональный и одновременно ассоциативный МК. В нем магическая сумма, равная 0,5n(1 + n·n) , дополнительно соблюдается по всем ломаным диагоналям, а каждая пара центрально противолежащих чисел дают в сумме 1+n·n. Пока известны ИМК нечетного порядка, начиная с n = 5. Исключение составляли два случая: n = 3(6k+5) и n = 3(6k+7) , где k = 0, 1, 2 , … , то есть было неясно - существуют ли, например, ИМК15 или ИМК21?

До настоящего времени отсутствовал универсальный принцип компоновки идеальных магических квадратов. Разными авторами были разработаны лишь частные приемы. Утвердилось мнение, будто при отмеченных двух случаях должны применяться особые, пока еще неизвестные, алгоритмы.

Тем не менее, я всегда стоял на позиции, что обязательно должен существовать единый подход к формированию идеальных магических квадратов любого нечетного порядка n > 3 .

И этот подход был, наконец, мною найден 14 ноября 2007 г.

Метод позволяет производить множество групп ИМК порядка n = 2k+1 , где k = 2, 3, 4, …

В данной статье поставлена цель доказать эффективность построения идеальных магических квадратов, в том числе и 15 х 15 , являющегося серьезным камнем преткновения для специалистов в этой области.

Раз мы задумали получить ассоциативный квадрат, то сразу можем поместить на центральном столбце три числа будущего идеального магического квадрата 15 х 15.

Самая верхняя ячейка – это 1

В самой нижней записываем n · n = 225 .

Центральная ячейка всего квадрата - очевидно, 0,5 (1 + n · n ) = 113

113

225

Рис. 1

[ Примечание. Крайние числа можно сближать к центру и тем самым добавить еще 0,5(n-1) – 1 схем расчета.]

Первая лента чисел P1 , P2 , P3 , . . . , P15 (голубые ячейки) производится ходом шахматного коня, как показано на Рис. 2. Затем осуществляется скачек на две клетки вниз и начинается вторая лента (бордовые ячейки). При этом число в первой бордовой клетке равно

(P2 - 1) n + P1, во второй (P2 - 1) n + P2 и так далее. Третья лента начнется с числа (P3 – 1) n + P1 и так далее…

↓

113

P10

P11

P12

P13

P14

P15

225

Рис. 2

Мы приняли P1 = 1. Однако у нас есть еще два конкретных числа : 113 и 225. Следовательно, имеется возможность определить Pv и Pw , зная траекторию расстановки чисел. Чтобы найти индексы v и w , достаточно центральный столбец чисто формально представить так:

P1	1
P9	2
P2	3
P10	4
P3	5
P11	6
P4	7
P12	8
P5	9
P13	10
P6	11
P14	12
P7	13
P15	14
P8	15

Рис. 3

Закономерность Pj , где индекс j = 1, 2, 3, …, n , очень простая – натуральный числовой ряд пишется через одну ячейку. Справа дана колонка с нумерацией строк. Мы видим, что v = 12 и w = 8 и, принимая во внимание лишь желтые ячейки, записываем:

P1 = 1

P12 = 8

P8 = 15

Теперь циклическую цепочку P1 , P2 , P3 , . . . , P15 организуем так, чтобы центральная P12 оказалась в центре строки:

P5 P6 P7 P8 P9 P10 P11 P12 P13 P14 P15 P1 P2 P3 P4

Относительно P12 значения остальных параметров должны быть симметричными по величине. Это необходимое, хотя и далеко недостаточное, условие существования пандиагонального квадрата.

Записываем очевидные уравнения:

P12 – P13 = P11 – P12

P13 – P14 = P10 – P11

P14 – P15 = P9 – P10

P15 – P1 = P8 – P9

P1 – P2 = P7 – P8

P2 – P3 = P6 – P7

P3 – P4 = P5 – P6

Решаем эту систему в математическом редакторе Maple:

solve({p12-p13=p11-p12,p13-p14=p10-p11,p14-p15=p9-p10,p15-p1=p8-p9,p1-p2=p7-p8,p2-p3=p6-p7,p3-p4=p5-p6,p1=1,p8=15,p12=8},[p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13,p14,p15]);

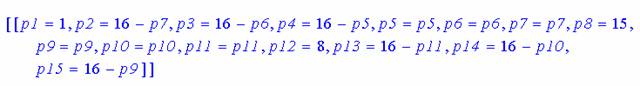
Получилось следующее:

Свободно варьируемые переменные: P5 , P6 , P7 , P9 , P10 , P11

Зависимые переменные:

P2 = 16 – P7

P3 = 16 – P6

P4 = 16 – P5 ( А )

P13 = 16 – P11

P14 = 16 – P10

P15 = 16 – P9

Жестко заданные константы: P1 = 1 , P8 = 15 , P12 = 8 .

P5 , P6 , P7 , P9 , P10 , P11 должны быть строго различными и набираться из любых чисел от 2 до 14, за исключением 8 .

Еще одно важное ограничение - не должно быть двух чисел, сумма которых равна 16. Систему уравнений можно не решать, если воспользоваться закольцованной графической схемой:

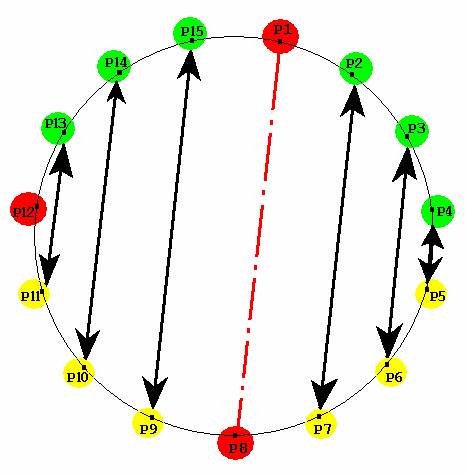
Рис. 4

Назначение цветных кружков:

Красные – это уже найденные конкретные параметры P1, P8, P12.

Желтые – это свободные варьируемые числа из набора от 2 до 14, за исключением 8 (выбранные числа не должны повторяться!).

Зеленые – это величины, зависимые от свободных (желтых) чисел. Двухсторонние стрелки показывают, какие пары чисел связаны друг с другом арифметическими формулами вида (А), Стрелки идут параллельно центральной красной линии, проведенной через P1 и (в данном конкретном случае) - P8 , характеризующей самое большое число в идеальном магическом квадрате. Желтые и зеленые цвета (но не обозначения ! ) могут меняться местами, причем одновременно все. Если такой обмен осуществлен, то это будет соответствовать следующей эквивалентной записи уравнений симметрии:

P12 – P13 = P11 – P12

P12 – P14 = P10 – P12

P12 – P15 = P9 – P12

P12 – P1 = P8 – P12

P12 – P2 = P7 – P12

P12 – P3 = P6 – P12

P12 – P4 = P5 – P12

Количество как желтых, так и зеленых параметров одинаково и равно

0,5 (n – 3)

Данная схема применима к любым нечетным n > 3 и полностью избавляет нас от составления большого числа линейных уравнений с последующим их решением.. Связь между сопряженными парами желтых и зеленых параметров – легче и не придумаешь:

Pa + Pb = n+1

В нашем случае n + 1 = 16 .

Внимание! Тот же результат мы получим, если примем за основу Рис.3. и в качестве свободных параметров возьмем те, что оказались в голубых ячейках. Параметры, помещенные в зеленых ячейках, будем вычислять по формулам вида (А), строго соблюдая зеркальность относительно P12 :

P5 = 16 – P4

P13 = 16 – P11

P6 = 16 – P3

P14 = 16 – P10

P7 = 16 – P2

P15 = 16 – P9

Вот в принципе и вся суть задачи нахождения идеальных магических квадратов 15 х 15 . Решим конкретный вариант.

Если из допустимого набора чисел 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14 выбрать, например, такие:

P5 = 2

P6 = 3

P7 = 6

P9 = 5

P10 = 7

P11 = 4

то оставшиеся 6 параметров окажутся равными:

P2 = 16 – P7 = 16 – 6 = 10

P3 = 16 – P6 = 16 – 3 = 13

P4 = 16 – P5 = 16 – 2 = 14

P13 = 16 – P11 = 16 – 4 = 12

P14 = 16 – P10 = 16 – 7 = 9

P15 = 16 – P9 = 16 – 5 = 11

Имеем в итоге следующую цепочку P1 , P2 , P3 , . . . , P15 :

1 10 13 14 2 3 6 15 5 7 4 8 12 9 11

Начертим окружность с 15-ю точками и соединим эти числа последовательно:

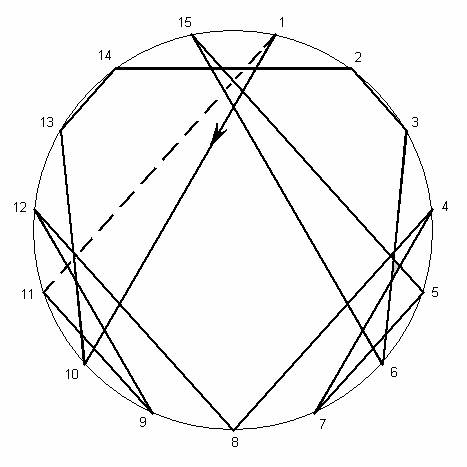
Рис. 5

Хорошо видно, что рисунок строго симметричный относительно вертикали, проведенной через точку 8. Угадать столь сложный путь какими-либо логическими соображениями практически невозможно. Это все равно, что подобрать шесть – девять цифр кода сейфа из набора двенадцати чисел. У меня составлена программа, позволяющая из тысяч кандидатов на решение, выбрать именно решения (для ИМК, у которых порядок матрицы не кратен трем, подобной выборки делать нет смысла - все варианты являются решениями задачи).

Зная код цепочки, уже не представляет особого труда построить идеальный магический квадрат методом движения шахматного коня с перескоками вниз через ячейку:

133	96	34	146	179	75	23	1	107	215	207	160	48	82	189
79	191	134	105	38	136	167	65	27	10	108	217	204	163	51
164	60	83	181	122	95	42	145	168	67	24	13	111	214	206
218	196	152	50	87	190	123	97	39	148	171	64	26	14	120
2	110	222	205	153	52	84	193	126	94	41	149	180	68	16
72	25	3	112	219	208	156	49	86	194	135	98	31	137	170
138	172	69	28	6	109	221	209	165	53	76	182	125	102	40
99	43	141	169	71	29	15	113	211	197	155	57	85	183	127
186	124	101	44	150	173	61	17	5	117	220	198	157	54	88
56	89	195	128	91	32	140	177	70	18	7	114	223	201	154
210	158	46	77	185	132	100	33	142	174	73	21	4	116	224
106	212	200	162	55	78	187	129	103	36	139	176	74	30	8
20	12	115	213	202	159	58	81	184	131	104	45	143	166	62
175	63	22	9	118	216	199	161	59	90	188	121	92	35	147
37	144	178	66	19	11	119	225	203	151	47	80	192	130	93

Рис. 6

Это - пандиагональный и ассоциативный магический квадрат пятнадцатого порядка, или ИМК15 . С такой же легкостью я находил ИМК21, ИМК23,…, ИМК33,…, ИМК39…

Повторюсь еще раз: если порядок n кратен 3 (как в рассматриваемом нами примере), то не для любых свободно варьируемых переменных существуют решения. Именно это я и имел в виду, когда выше говорил о недостаточности обеспечения одной только симметрии кругового графика на Рис. 5. Хотя, правда, полный перебор перестановок чисел позволяет находить довольно много желанных матриц.

Изложенным методом при n = 5 было найдено 2 вида ИМК; при n = 7 - 8 видов, при n = 9 - 4 различных ИМК, при n = 11 - 408 , а уже при n = 15 - ровно 1024 положительных результата (я же построил “только” 32 ИМК-15).. Количество ИМК21 уже 110592.

Приведу еще один красивый пример идеального магического квадрата 15 x 15 :

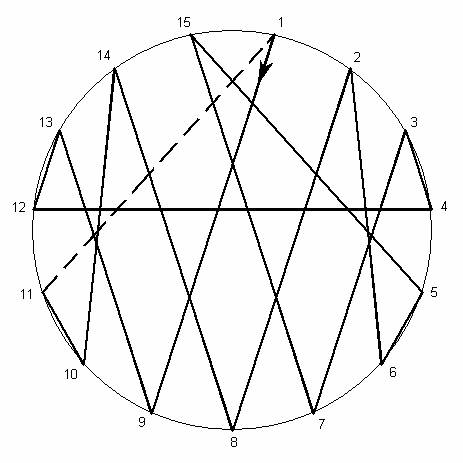
Рис. 7

148	82	32	131	207	75	53	1	109	215	179	159	18	96	190
92	191	147	90	38	121	199	65	59	9	108	216	175	163	22
162	30	98	181	139	80	44	129	198	66	55	13	112	212	176
218	166	154	20	104	189	138	81	40	133	202	62	56	12	120
4	110	224	174	153	21	100	193	142	77	41	132	210	68	46
74	54	3	111	220	178	157	17	101	192	150	83	31	124	200
123	201	70	58	7	107	221	177	165	23	91	184	140	89	39
85	43	127	197	71	57	15	113	211	169	155	29	99	183	141
187	137	86	42	135	203	61	49	5	119	219	168	156	25	103
26	102	195	143	76	34	125	209	69	48	6	115	223	172	152
180	158	16	94	185	149	84	33	126	205	73	52	2	116	222
106	214	170	164	24	93	186	145	88	37	122	206	72	60	8
50	14	114	213	171	160	28	97	182	146	87	45	128	196	64
204	63	51	10	118	217	167	161	27	105	188	136	79	35	134
36	130	208	67	47	11	117	225	173	151	19	95	194	144	78

Рис. 8

Продемонстрируем свойства пандиагональности и ассоциативности этой матрицы:

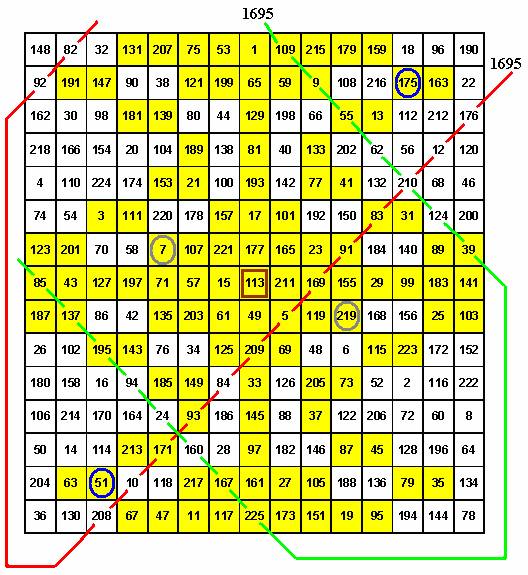
Рис. 9

Сумма чисел по любой ломаной диагонали (см., например, либо красную, либо зеленую линию на Рис. 9) равна магическому значению 1695. Числа в синих кружках 175 и 51, которые симметрично расположены относительно центра 113 , образуют сумму 226; точно такую же сумму обеспечивают центрально противолежащие числа 7 и 219 (в серых кружках). Данным свойством обладают все 0,5 (n · n – 1) пары чисел матрицы. Центральная ячейка, сложенная сама с собой, также дает число 226.

Конечно, крайне интересно приведенные выше примеры подвергнуть различным преобразованиям, в ходе которых получились бы новые четно-нечетные мозаики идеальных магических квадратов. Возможно, в процессе такой благородной работы и выявится самый базовый ИМК – единственный и неповторимый.

С целью более полного понимания предложенной модели применим описанную методику для ИМК9 , но с несколько иной начальной схемой:




				1
				41
				81

Рис. 10

Попытаемся в рамках принятого ограничения найти все решения, которые позволит дать мой метод . Строим центральный столбец:

P4	1
P9	2
P5	3
P1	4	1
P6	5
P2	6	9
P7	7
P3	8
P8	9

Рис. 11

По этой схеме определяем значения трех параметров: P1 = 1 , P6 = 5 , P2 = 9 .

Свойства остальных Pj выявим, рассмотрев круговую структуру:

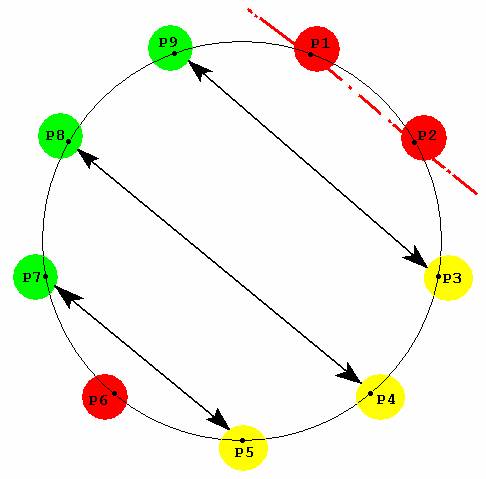
Рис. 12

Отсюда видно, что свободные параметры - это P3, P4, P5 ( желтые кружочки) , а остальные (зеленые) – зависимые параметры, определяемые по формулам:

P9 = 10 – P3

P8 = 10 – P4

P7 = 10 – P5

Свободные параметры можно заполнять любыми числами из набора 2, 3, 4, 6, 7, 8 . Для существенного сокращения числа вариантов, из этого набора смело исключаем пары 4 и 6 , 3 и 7 , 2 и 8 ( их сумма равна 10, что приведет к неизбежному дублированию чисел в полной цепочке).

Если распределять числа только по возрастанию, то возможны 8 вариантов:

2 3 4

2 3 6

2 4 7

2 6 7

3 4 8

3 6 8

4 7 8

6 7 8

Каждая тройка чисел допускает 3! = 6 перестановок. Поэтому общее число допустимых комбинаций P3, P4, P5 равно 48. Из них лишь четыре тройки оказались решениями поставленной задачи: 3 8 4 , 7 8 4 , 3 6 2 , 7 6 2 . Я это выявил путем проверки всех 48 вариаций. Возможно, существуют какие-то строгие связи между найденными тройками чисел и порядком n . Если их обнаружить, то задача еще более упростится.

Цепочки чисел следующие:

1 9 3 8 4 5 6 2 7

1 9 7 8 4 5 6 2 3

1 9 3 6 2 5 8 4 7

1 9 7 6 2 5 8 4 3

Рассмотрим решения более детально.

1 9 3 8 4 5 6 2 7

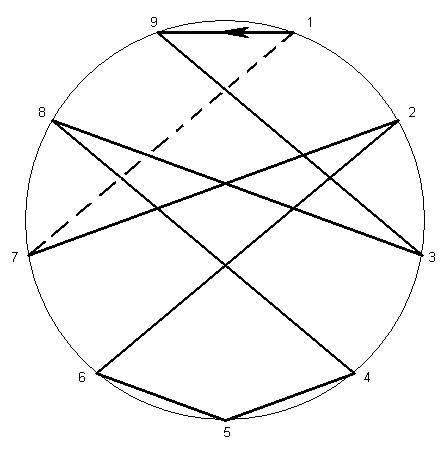
Рис. 13

30	46	56	77	71	45	16	6	22
2	23	35	54	61	78	67	39	10
44	18	7	24	31	48	55	74	68
79	69	40	12	1	20	32	53	63
49	57	73	65	41	17	9	25	33
19	29	50	62	81	70	42	13	3
14	8	27	34	51	58	75	64	38
72	43	15	4	21	28	47	59	80
60	76	66	37	11	5	26	36	52

Рис. 14

1 9 7 8 4 5 6 2 3

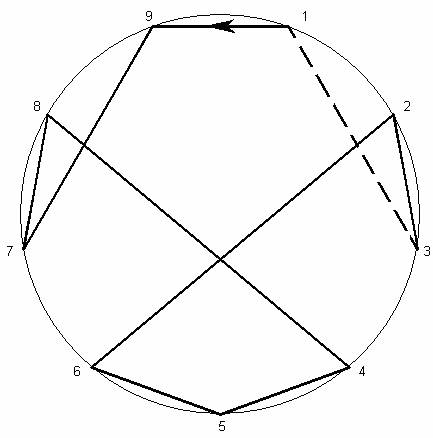
Рис. 15

34	46	20	77	71	45	12	6	58
2	59	35	54	21	78	67	43	10
44	18	3	60	31	52	19	74	68
75	69	40	16	1	56	32	53	27
49	25	73	65	41	17	9	57	33
55	29	50	26	81	66	42	13	7
14	8	63	30	51	22	79	64	38
72	39	15	4	61	28	47	23	80
24	76	70	37	11	5	62	36	48

Рис. 16

1 9 3 6 2 5 8 4 7

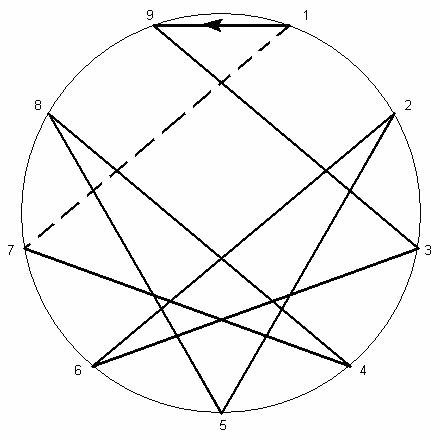
Рис. 17

12	64	58	77	51	45	34	8	20
4	23	15	72	61	80	47	39	28
42	36	7	26	11	66	55	76	50
79	53	38	30	1	22	14	69	63
65	57	73	49	41	33	9	25	17
19	13	68	60	81	52	44	29	3
32	6	27	16	71	56	75	46	40
54	43	35	2	21	10	67	59	78
62	74	48	37	31	5	24	18	70

Рис. 18

1 9 7 6 2 5 8 4 3

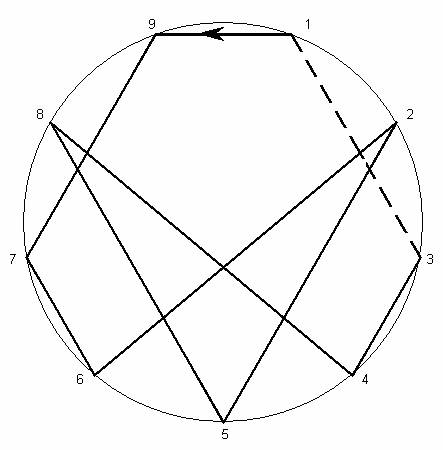
Рис. 19

16	64	22	77	51	45	30	8	56
4	59	15	72	21	80	47	43	28
42	36	3	62	11	70	19	76	50
75	53	38	34	1	58	14	69	27
65	25	73	49	41	33	9	57	17
55	13	68	24	81	48	44	29	7
32	6	63	12	71	20	79	46	40
54	39	35	2	61	10	67	23	78
26	74	52	37	31	5	60	18	66

Рис. 20

Анализ примеров построения ИМК9 позволяет сформулировать компактный способ выбора нужных цепочек чисел, который сводится к чисто арифметической задаче. Покажем это в самом общем виде:

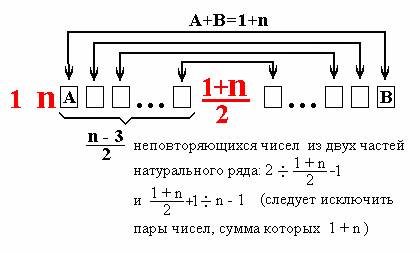
Рис. 21

С точки зрения программирования данная задача является элементарной.

Ценность методики заключается в возможности находить все идеальные магические квадраты, получаемые ходами шахматного коня (их количество каждый раз равно n ) с последующим перескоком через строку вниз.

Проверим схему на Рис. 21 при составлении ИМК15

Если согласно данной схеме рассчитать варианты P3, P4, P5, P6, P7, P8 по возрастанию величин, то по программе:

rem Определение числа вариантов ИМК-15

open #1,"15-N_var.txt","w"

dim p(100),t(100),t1(100)

n=15:n1=(n-3)/2

rem Формирование чисел, участвующих в перестановках

for i=1 to n-2:if i<=n1 then:p(i)=i+1:fi

if i>n1+1 then:p(i-1)=i+1:fi:next i

for i=1 to n-3:print p(i);:next i:print:print

rem все возможные варианты чисел в порядке возрастания

for i1=1 to n1+1

for i2=i1+1 to n1+2

for i3=i2+1 to n1+3

for i4=i3+1 to n1+4

for i5=i4+1 to n1+5

for i6=i5+1 to n1+6

rem Блок фильтрации ненужных пар чисел, дающих в сумме n+1

k=0

t(1)=p(i1):t(2)=p(i2):t(3)=p(i3):t(4)=p(i4):t(5)=p(i5):t(6)=p(i6)

for i=1 to n1:t1(i)=t(i):next i

for i=1 to n1:for j=1 to n1

if i<>j then:if t(i)+t(j)=n+1 then k=1:fi:fi:next j:next i

if k<>1 then s=s+1:print s;:print #1,s;:print #1,",";

for i=1 to n1:print t(i);:print #1,t(i);:if i<>n1 then print #1,",";:fi:next i:print:print #1:fi

next i6:next i5:next i4:next i3:next i2:next i1

получим 64 варианта.

№	P3	P4	P5	P6	P7	P8	№	P3	P4	P5	P6	P7	P8
1	2	3	4	5	6	7	33	3	4	5	6	7	14
2	2	3	4	5	6	9	34	3	4	5	6	9	14
3	2	3	4	5	7	10	35	3	4	5	7	10	14
4	2	3	4	5	9	10	36	3	4	5	9	10	14
5	2	3	4	6	7	11	37	3	4	6	7	11	14
6	2	3	4	6	9	11	38	3	4	6	9	11	14
7	2	3	4	7	10	11	39	3	4	7	10	11	14
8	2	3	4	9	10	11	40	3	4	9	10	11	14
9	2	3	5	6	7	12	41	3	5	6	7	12	14
10	2	3	5	6	9	12	42	3	5	6	9	12	14
11	2	3	5	7	10	12	43	3	5	7	10	12	14
12	2	3	5	9	10	12	44	3	5	9	10	12	14
13	2	3	6	7	11	12	45	3	6	7	11	12	14
14	2	3	6	9	11	12	46	3	6	9	11	12	14
15	2	3	7	10	11	12	47	3	7	10	11	12	14
16	2	3	9	10	11	12	48	3	9	10	11	12	14
17	2	4	5	6	7	13	49	4	5	6	7	13	14
18	2	4	5	6	9	13	50	4	5	6	9	13	14
19	2	4	5	7	10	13	51	4	5	7	10	13	14
20	2	4	5	9	10	13	52	4	5	9	10	13	14
21	2	4	6	7	11	13	53	4	6	7	11	13	14
22	2	4	6	9	11	13	54	4	6	9	11	13	14
23	2	4	7	10	11	13	55	4	7	10	11	13	14
24	2	4	9	10	11	13	56	4	9	10	11	13	14
25	2	5	6	7	12	13	57	5	6	7	12	13	14
26	2	5	6	9	12	13	58	5	6	9	12	13	14
27	2	5	7	10	12	13	59	5	7	10	12	13	14
28	2	5	9	10	12	13	60	5	9	10	12	13	14
29	2	6	7	11	12	13	61	6	7	11	12	13	14
30	2	6	9	11	12	13	62	6	9	11	12	13	14
31	2	7	10	11	12	13	63	7	10	11	12	13	14
32	2	9	10	11	12	13	64	9	10	11	12	13	14

Общее число схем: N = 64 * 6! = 46080

Число вариантов ИМК15 - 1024

Выберем произвольную строку, например, № 43. Из 6!=720 перестановок удается найти 16 решений (как и для любой другой строки). Вот эти удивительные цепочки чисел:

1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11	P12	P13	P14	P15
1	15	7	10	12	3	14	5	8	11	2	13	4	6	9
1	15	10	12	3	14	5	7	8	9	11	2	13	4	6
1	15	3	14	5	7	10	12	8	4	6	9	11	2	13
1	15	14	5	7	10	12	3	8	13	4	6	9	11	2
1	15	3	10	5	7	14	12	8	4	2	9	11	6	13
1	15	10	5	7	14	12	3	8	13	4	2	9	11	6
1	15	7	14	12	3	10	5	8	11	6	13	4	2	9
1	15	14	12	3	10	5	7	8	9	11	6	13	4	2
1	15	7	10	5	3	14	12	8	4	2	13	11	6	9
1	15	10	5	3	14	12	7	8	9	4	2	13	11	6
1	15	3	14	12	7	10	5	8	11	6	9	4	2	13
1	15	14	12	7	10	5	3	8	13	11	6	9	4	2
1	15	3	10	12	7	14	5	8	11	2	9	4	6	13
1	15	10	12	7	14	5	3	8	13	11	2	9	4	6
1	15	7	14	5	3	10	12	8	4	6	13	11	2	9
1	15	14	5	3	10	12	7	8	9	4	6	13	11	2

Построим 16 ИМК15:

№ 43 - 1

24, 205, 95, 88, 151, 42, 218, 49, 120, 168, 11, 186, 67, 149, 122

140, 133, 16, 207, 98, 79, 165, 33, 221, 51, 112, 179, 2, 189, 70

181, 72, 143, 124, 30, 198, 101, 81, 157, 44, 212, 54, 115, 170, 13

173, 4, 195, 63, 146, 126, 22, 209, 92, 84, 160, 35, 223, 46, 117

60, 108, 176, 6, 187, 74, 137, 129, 25, 200, 103, 76, 162, 38, 214

41, 216, 52, 119, 167, 9, 190, 65, 148, 121, 27, 203, 94, 90, 153

82, 164, 32, 219, 55, 110, 178, 1, 192, 68, 139, 135, 18, 206, 96

197, 99, 85, 155, 43, 211, 57, 113, 169, 15, 183, 71, 141, 127, 29

130, 20, 208, 91, 87, 158, 34, 225, 48, 116, 171, 7, 194, 62, 144

73, 136, 132, 23, 199, 105, 78, 161, 36, 217, 59, 107, 174, 10, 185

12, 188, 64, 150, 123, 26, 201, 97, 89, 152, 39, 220, 50, 118, 166

109, 180, 3, 191, 66, 142, 134, 17, 204, 100, 80, 163, 31, 222, 53

213, 56, 111, 172, 14, 182, 69, 145, 125, 28, 196, 102, 83, 154, 45

156, 37, 224, 47, 114, 175, 5, 193, 61, 147, 128, 19, 210, 93, 86

104, 77, 159, 40, 215, 58, 106, 177, 8, 184, 75, 138, 131, 21, 202

№ 43 - 2

156, 72, 142, 47, 121, 198, 218, 193, 120, 44, 9, 19, 100, 170, 86

172, 77, 151, 63, 143, 58, 135, 209, 219, 184, 115, 35, 11, 21, 102

16, 93, 173, 88, 165, 74, 144, 49, 130, 200, 221, 186, 117, 37, 2

38, 13, 30, 104, 174, 79, 160, 65, 146, 51, 132, 202, 212, 181, 108

195, 119, 39, 4, 25, 95, 176, 81, 162, 67, 137, 46, 123, 203, 223

204, 214, 190, 110, 41, 6, 27, 97, 167, 76, 153, 68, 148, 60, 134

55, 125, 206, 216, 192, 112, 32, 1, 18, 98, 178, 90, 164, 69, 139

71, 141, 57, 127, 197, 211, 183, 113, 43, 15, 29, 99, 169, 85, 155

87, 157, 62, 136, 48, 128, 208, 225, 194, 114, 34, 10, 20, 101, 171

92, 166, 78, 158, 73, 150, 59, 129, 199, 220, 185, 116, 36, 12, 22

3, 23, 103, 180, 89, 159, 64, 145, 50, 131, 201, 222, 187, 107, 31

118, 45, 14, 24, 94, 175, 80, 161, 66, 147, 52, 122, 196, 213, 188

224, 189, 109, 40, 5, 26, 96, 177, 82, 152, 61, 138, 53, 133, 210

124, 205, 215, 191, 111, 42, 7, 17, 91, 168, 83, 163, 75, 149, 54

140, 56, 126, 207, 217, 182, 106, 33, 8, 28, 105, 179, 84, 154, 70

№ 43 - 3

88, 149, 42, 24, 46, 95, 218, 161, 120, 67, 4, 122, 168, 205, 186

207, 189, 76, 140, 38, 26, 60, 97, 214, 152, 108, 70, 6, 133, 179

121, 170, 203, 191, 90, 142, 34, 17, 48, 100, 216, 163, 119, 72, 9

68, 11, 135, 172, 199, 182, 78, 145, 36, 28, 59, 102, 219, 151, 110

165, 112, 64, 2, 123, 175, 201, 193, 89, 147, 39, 16, 50, 98, 221

94, 212, 153, 115, 66, 13, 134, 177, 204, 181, 80, 143, 41, 30, 52

18, 55, 96, 223, 164, 117, 69, 1, 125, 173, 206, 195, 82, 139, 32

141, 43, 29, 57, 99, 211, 155, 113, 71, 15, 127, 169, 197, 183, 85

194, 87, 144, 31, 20, 53, 101, 225, 157, 109, 62, 3, 130, 171, 208

174, 196, 185, 83, 146, 45, 22, 49, 92, 213, 160, 111, 73, 14, 132

5, 128, 176, 210, 187, 79, 137, 33, 25, 51, 103, 224, 162, 114, 61

116, 75, 7, 124, 167, 198, 190, 81, 148, 44, 27, 54, 91, 215, 158

217, 154, 107, 63, 10, 126, 178, 209, 192, 84, 136, 35, 23, 56, 105

47, 93, 220, 156, 118, 74, 12, 129, 166, 200, 188, 86, 150, 37, 19

40, 21, 58, 104, 222, 159, 106, 65, 8, 131, 180, 202, 184, 77, 138

№ 43 - 4

47, 170, 198, 156, 181, 142, 218, 129, 120, 100, 13, 86, 44, 72, 19

63, 21, 46, 172, 203, 159, 195, 145, 223, 131, 119, 102, 4, 77, 35

76, 37, 68, 24, 60, 175, 208, 161, 194, 147, 214, 122, 110, 93, 6

98, 9, 90, 40, 73, 26, 59, 177, 199, 152, 185, 138, 216, 121, 112

135, 115, 103, 11, 89, 42, 64, 17, 50, 168, 201, 151, 187, 143, 219

148, 221, 134, 117, 94, 2, 80, 33, 66, 16, 52, 173, 204, 165, 190

164, 192, 139, 212, 125, 108, 96, 1, 82, 38, 69, 30, 55, 178, 206

169, 197, 155, 183, 141, 211, 127, 113, 99, 15, 85, 43, 71, 29, 57

20, 48, 171, 196, 157, 188, 144, 225, 130, 118, 101, 14, 87, 34, 62

36, 61, 22, 53, 174, 210, 160, 193, 146, 224, 132, 109, 92, 5, 78

7, 83, 39, 75, 25, 58, 176, 209, 162, 184, 137, 215, 123, 111, 91

114, 105, 10, 88, 41, 74, 27, 49, 167, 200, 153, 186, 136, 217, 128

220, 133, 116, 104, 12, 79, 32, 65, 18, 51, 166, 202, 158, 189, 150

191, 149, 222, 124, 107, 95, 3, 81, 31, 67, 23, 54, 180, 205, 163

207, 154, 182, 140, 213, 126, 106, 97, 8, 84, 45, 70, 28, 56, 179

№ 43 - 5

28, 205, 42, 84, 46, 95, 218, 161, 120, 67, 4, 126, 168, 149, 182

147, 189, 16, 200, 38, 86, 60, 97, 214, 156, 108, 74, 2, 133, 175

121, 170, 143, 191, 30, 202, 34, 81, 48, 104, 212, 163, 115, 72, 9

68, 11, 135, 172, 139, 186, 18, 209, 32, 88, 55, 102, 219, 151, 110

165, 112, 64, 6, 123, 179, 137, 193, 25, 207, 39, 76, 50, 98, 221

94, 216, 153, 119, 62, 13, 130, 177, 144, 181, 20, 203, 41, 90, 52

78, 59, 92, 223, 160, 117, 69, 1, 125, 173, 146, 195, 22, 199, 36

197, 43, 85, 57, 99, 211, 155, 113, 71, 15, 127, 169, 141, 183, 29

190, 27, 204, 31, 80, 53, 101, 225, 157, 109, 66, 3, 134, 167, 148

174, 136, 185, 23, 206, 45, 82, 49, 96, 213, 164, 107, 73, 10, 132

5, 128, 176, 150, 187, 19, 201, 33, 89, 47, 103, 220, 162, 114, 61

116, 75, 7, 124, 171, 138, 194, 17, 208, 40, 87, 54, 91, 215, 158

217, 154, 111, 63, 14, 122, 178, 145, 192, 24, 196, 35, 83, 56, 105

51, 93, 224, 152, 118, 70, 12, 129, 166, 140, 188, 26, 210, 37, 79

44, 77, 58, 100, 222, 159, 106, 65, 8, 131, 180, 142, 184, 21, 198

№ 43 - 6

51, 170, 138, 152, 181, 202, 218, 129, 120, 104, 13, 26, 40, 72, 79

63, 77, 46, 172, 143, 159, 195, 209, 223, 131, 115, 102, 4, 21, 35

16, 37, 68, 84, 60, 179, 148, 161, 190, 207, 214, 126, 110, 93, 2

98, 9, 30, 44, 73, 86, 55, 177, 139, 156, 185, 198, 212, 121, 112

135, 119, 103, 11, 25, 42, 64, 81, 50, 168, 137, 151, 187, 203, 219

208, 221, 130, 117, 94, 6, 20, 33, 62, 76, 52, 173, 144, 165, 194

160, 192, 199, 216, 125, 108, 92, 1, 22, 38, 69, 90, 59, 178, 146

169, 141, 155, 183, 197, 211, 127, 113, 99, 15, 29, 43, 71, 85, 57

80, 48, 167, 136, 157, 188, 204, 225, 134, 118, 101, 10, 27, 34, 66

32, 61, 82, 53, 174, 150, 164, 193, 206, 220, 132, 109, 96, 5, 18

7, 23, 39, 75, 89, 58, 176, 145, 162, 184, 201, 215, 123, 107, 91

114, 105, 14, 28, 41, 70, 87, 49, 171, 140, 153, 182, 196, 217, 128

224, 133, 116, 100, 12, 19, 36, 65, 78, 47, 166, 142, 158, 189, 210

191, 205, 222, 124, 111, 95, 3, 17, 31, 67, 83, 54, 180, 149, 163

147, 154, 186, 200, 213, 122, 106, 97, 8, 24, 45, 74, 88, 56, 175

№ 43 - 7

84, 149, 95, 28, 151, 42, 218, 49, 120, 168, 11, 182, 67, 205, 126

200, 133, 76, 147, 98, 19, 165, 33, 221, 47, 112, 175, 6, 189, 74

181, 72, 203, 124, 90, 138, 101, 17, 157, 40, 216, 54, 119, 170, 13

173, 4, 195, 63, 206, 122, 82, 145, 96, 24, 164, 35, 223, 46, 117

60, 108, 176, 2, 187, 70, 201, 129, 89, 140, 103, 16, 162, 38, 214

41, 212, 52, 115, 171, 9, 194, 65, 208, 121, 87, 143, 94, 30, 153

22, 160, 36, 219, 59, 110, 178, 1, 192, 68, 199, 135, 78, 146, 92

141, 99, 29, 155, 43, 211, 57, 113, 169, 15, 183, 71, 197, 127, 85

134, 80, 148, 91, 27, 158, 34, 225, 48, 116, 167, 7, 190, 66, 204

73, 196, 132, 83, 139, 105, 18, 161, 32, 217, 55, 111, 174, 14, 185

12, 188, 64, 210, 123, 86, 137, 97, 25, 156, 39, 224, 50, 118, 166

109, 180, 3, 191, 62, 202, 130, 81, 144, 104, 20, 163, 31, 222, 53

213, 56, 107, 172, 10, 186, 69, 209, 125, 88, 136, 102, 23, 154, 45

152, 37, 220, 51, 114, 179, 5, 193, 61, 207, 128, 79, 150, 93, 26

100, 21, 159, 44, 215, 58, 106, 177, 8, 184, 75, 198, 131, 77, 142

№ 43 - 8

152, 72, 202, 51, 121, 138, 218, 193, 120, 40, 9, 79, 104, 170, 26

172, 21, 151, 63, 203, 58, 135, 145, 219, 184, 119, 35, 11, 77, 102

76, 93, 173, 28, 165, 70, 204, 49, 134, 140, 221, 182, 117, 37, 6

38, 13, 90, 100, 174, 19, 164, 65, 206, 47, 132, 142, 216, 181, 108

195, 115, 39, 4, 89, 95, 176, 17, 162, 67, 201, 46, 123, 143, 223

144, 214, 194, 110, 41, 2, 87, 97, 171, 16, 153, 68, 208, 60, 130

59, 125, 146, 212, 192, 112, 36, 1, 78, 98, 178, 30, 160, 69, 199

71, 197, 57, 127, 141, 211, 183, 113, 43, 15, 85, 99, 169, 29, 155

27, 157, 66, 196, 48, 128, 148, 225, 190, 114, 34, 14, 80, 101, 167

96, 166, 18, 158, 73, 210, 55, 129, 139, 224, 185, 116, 32, 12, 82

3, 83, 103, 180, 25, 159, 64, 209, 50, 131, 137, 222, 187, 111, 31

118, 45, 10, 84, 94, 179, 20, 161, 62, 207, 52, 126, 136, 213, 188

220, 189, 109, 44, 5, 86, 92, 177, 22, 156, 61, 198, 53, 133, 150

124, 149, 215, 191, 107, 42, 7, 81, 91, 168, 23, 163, 75, 205, 54

200, 56, 122, 147, 217, 186, 106, 33, 8, 88, 105, 175, 24, 154, 74

№ 43 - 9

24, 205, 102, 88, 46, 35, 218, 161, 120, 63, 4, 186, 172, 149, 122

147, 133, 16, 200, 98, 86, 60, 33, 214, 156, 112, 74, 2, 189, 175

181, 170, 143, 131, 30, 198, 94, 81, 52, 44, 212, 159, 115, 72, 13

68, 11, 195, 168, 139, 126, 22, 209, 92, 84, 55, 42, 223, 151, 110

165, 108, 64, 6, 187, 179, 137, 129, 25, 207, 103, 76, 50, 38, 221

34, 216, 157, 119, 62, 9, 190, 177, 148, 121, 20, 203, 101, 90, 48

82, 59, 32, 219, 160, 117, 73, 1, 185, 173, 146, 135, 18, 199, 96

197, 99, 85, 57, 43, 211, 155, 113, 71, 15, 183, 169, 141, 127, 29

130, 27, 208, 91, 80, 53, 41, 225, 153, 109, 66, 7, 194, 167, 144

178, 136, 125, 23, 206, 105, 78, 49, 36, 217, 164, 107, 69, 10, 192

5, 188, 176, 150, 123, 19, 201, 97, 89, 47, 39, 220, 162, 118, 61

116, 75, 3, 184, 171, 142, 134, 17, 204, 100, 87, 58, 31, 215, 158

213, 154, 111, 67, 14, 182, 174, 145, 132, 28, 196, 95, 83, 56, 45

51, 37, 224, 152, 114, 70, 12, 193, 166, 140, 128, 26, 210, 93, 79

104, 77, 54, 40, 222, 163, 106, 65, 8, 191, 180, 138, 124, 21, 202

№ 43 - 10

51, 170, 142, 152, 121, 198, 218, 193, 120, 44, 9, 26, 100, 72, 79

67, 77, 46, 168, 143, 163, 135, 209, 219, 191, 115, 42, 4, 21, 95

16, 93, 68, 88, 60, 179, 144, 161, 130, 207, 214, 186, 110, 37, 2

38, 13, 30, 104, 69, 86, 55, 177, 139, 156, 125, 202, 212, 181, 108

195, 119, 39, 11, 25, 102, 64, 81, 50, 172, 137, 151, 123, 203, 223

204, 221, 190, 117, 34, 6, 20, 97, 62, 76, 48, 173, 148, 165, 134

160, 132, 199, 216, 185, 112, 32, 1, 18, 98, 73, 90, 59, 174, 146

169, 141, 155, 127, 197, 211, 183, 113, 43, 15, 29, 99, 71, 85, 57

80, 52, 167, 136, 153, 128, 208, 225, 194, 114, 41, 10, 27, 94, 66

92, 61, 78, 53, 178, 150, 164, 129, 206, 220, 192, 109, 36, 5, 22

3, 23, 103, 75, 89, 54, 176, 145, 162, 124, 201, 215, 187, 107, 31

118, 45, 14, 24, 101, 70, 87, 49, 171, 140, 157, 122, 196, 213, 188

224, 189, 116, 40, 12, 19, 96, 65, 82, 47, 166, 138, 158, 133, 210

131, 205, 222, 184, 111, 35, 7, 17, 91, 63, 83, 58, 180, 149, 159

147, 154, 126, 200, 217, 182, 106, 33, 8, 28, 105, 74, 84, 56, 175

№ 43 - 11

88, 149, 35, 24, 151, 102, 218, 49, 120, 172, 11, 122, 63, 205, 186

200, 189, 76, 147, 38, 19, 165, 97, 221, 47, 108, 175, 6, 133, 74

121, 72, 203, 184, 90, 142, 41, 17, 153, 100, 216, 58, 119, 170, 9

173, 4, 135, 67, 206, 182, 78, 145, 36, 28, 164, 95, 219, 46, 117

60, 112, 176, 2, 123, 70, 201, 193, 89, 140, 39, 16, 162, 98, 214

101, 212, 48, 115, 171, 13, 134, 65, 204, 181, 87, 143, 34, 30, 157

18, 160, 96, 223, 59, 110, 174, 1, 132, 68, 199, 195, 82, 146, 32

141, 43, 29, 155, 99, 211, 57, 113, 169, 15, 127, 71, 197, 183, 85

194, 80, 144, 31, 27, 158, 94, 225, 52, 116, 167, 3, 130, 66, 208

69, 196, 192, 83, 139, 45, 22, 161, 92, 213, 55, 111, 178, 14, 125

12, 128, 64, 210, 187, 86, 137, 33, 25, 156, 103, 224, 50, 114, 166

109, 180, 7, 131, 62, 198, 190, 81, 148, 44, 20, 159, 91, 222, 53

217, 56, 107, 168, 10, 126, 73, 209, 185, 84, 136, 42, 23, 154, 105

152, 93, 220, 51, 118, 179, 5, 129, 61, 207, 188, 79, 150, 37, 26

40, 21, 163, 104, 215, 54, 106, 177, 8, 124, 75, 202, 191, 77, 138

№ 43 - 12

152, 72, 198, 51, 181, 142, 218, 129, 120, 100, 13, 79, 44, 170, 26

168, 21, 151, 67, 203, 54, 195, 145, 223, 124, 119, 95, 11, 77, 42

76, 37, 173, 24, 165, 70, 208, 49, 194, 140, 221, 122, 117, 93, 6

98, 9, 90, 40, 178, 19, 164, 65, 206, 47, 192, 138, 216, 121, 112

135, 115, 103, 4, 89, 35, 176, 17, 162, 63, 201, 46, 187, 143, 219

148, 214, 134, 110, 101, 2, 87, 33, 171, 16, 157, 68, 204, 60, 190

59, 185, 146, 212, 132, 108, 96, 1, 82, 38, 174, 30, 160, 73, 199

71, 197, 57, 183, 141, 211, 127, 113, 99, 15, 85, 43, 169, 29, 155

27, 153, 66, 196, 52, 188, 144, 225, 130, 118, 94, 14, 80, 41, 167

36, 166, 22, 158, 69, 210, 55, 193, 139, 224, 125, 116, 92, 12, 78

7, 83, 39, 180, 25, 163, 64, 209, 50, 191, 137, 222, 123, 111, 91

114, 105, 10, 88, 34, 179, 20, 161, 62, 207, 48, 186, 136, 217, 128

220, 133, 109, 104, 5, 86, 32, 177, 18, 156, 61, 202, 53, 189, 150

184, 149, 215, 131, 107, 102, 3, 81, 31, 172, 23, 159, 75, 205, 58

200, 56, 182, 147, 213, 126, 106, 97, 8, 84, 45, 175, 28, 154, 74

№ 43 - 13

28, 205, 35, 84, 151, 102, 218, 49, 120, 172, 11, 126, 63, 149, 182

140, 189, 16, 207, 38, 79, 165, 97, 221, 51, 108, 179, 2, 133, 70

121, 72, 143, 184, 30, 202, 41, 81, 153, 104, 212, 58, 115, 170, 9

173, 4, 135, 67, 146, 186, 18, 209, 32, 88, 160, 95, 219, 46, 117

60, 112, 176, 6, 123, 74, 137, 193, 25, 200, 39, 76, 162, 98, 214

101, 216, 48, 119, 167, 13, 130, 65, 144, 181, 27, 203, 34, 90, 157

78, 164, 92, 223, 55, 110, 174, 1, 132, 68, 139, 195, 22, 206, 36

197, 43, 85, 155, 99, 211, 57, 113, 169, 15, 127, 71, 141, 183, 29

190, 20, 204, 31, 87, 158, 94, 225, 52, 116, 171, 3, 134, 62, 148

69, 136, 192, 23, 199, 45, 82, 161, 96, 213, 59, 107, 178, 10, 125

12, 128, 64, 150, 187, 26, 201, 33, 89, 152, 103, 220, 50, 114, 166

109, 180, 7, 131, 66, 138, 194, 17, 208, 40, 80, 159, 91, 222, 53

217, 56, 111, 168, 14, 122, 73, 145, 185, 24, 196, 42, 83, 154, 105

156, 93, 224, 47, 118, 175, 5, 129, 61, 147, 188, 19, 210, 37, 86

44, 77, 163, 100, 215, 54, 106, 177, 8, 124, 75, 142, 191, 21, 198

№ 43 - 14

156, 72, 138, 47, 181, 202, 218, 129, 120, 104, 13, 19, 40, 170, 86

168, 77, 151, 67, 143, 54, 195, 209, 223, 124, 115, 95, 11, 21, 42

16, 37, 173, 84, 165, 74, 148, 49, 190, 200, 221, 126, 117, 93, 2

98, 9, 30, 44, 178, 79, 160, 65, 146, 51, 192, 198, 212, 121, 112

135, 119, 103, 4, 25, 35, 176, 81, 162, 63, 137, 46, 187, 203, 219

208, 214, 130, 110, 101, 6, 27, 33, 167, 76, 157, 68, 144, 60, 194

55, 185, 206, 216, 132, 108, 92, 1, 22, 38, 174, 90, 164, 73, 139

71, 141, 57, 183, 197, 211, 127, 113, 99, 15, 29, 43, 169, 85, 155

87, 153, 62, 136, 52, 188, 204, 225, 134, 118, 94, 10, 20, 41, 171

32, 166, 82, 158, 69, 150, 59, 193, 199, 220, 125, 116, 96, 12, 18

7, 23, 39, 180, 89, 163, 64, 145, 50, 191, 201, 222, 123, 107, 91

114, 105, 14, 28, 34, 175, 80, 161, 66, 147, 48, 182, 196, 217, 128

224, 133, 109, 100, 5, 26, 36, 177, 78, 152, 61, 142, 53, 189, 210

184, 205, 215, 131, 111, 102, 3, 17, 31, 172, 83, 159, 75, 149, 58

140, 56, 186, 207, 213, 122, 106, 97, 8, 24, 45, 179, 88, 154, 70

№ 43 - 15

84, 149, 102, 28, 46, 35, 218, 161, 120, 63, 4, 182, 172, 205, 126

207, 133, 76, 140, 98, 26, 60, 33, 214, 152, 112, 70, 6, 189, 179

181, 170, 203, 131, 90, 138, 94, 17, 52, 40, 216, 159, 119, 72, 13

68, 11, 195, 168, 199, 122, 82, 145, 96, 24, 59, 42, 223, 151, 110

165, 108, 64, 2, 187, 175, 201, 129, 89, 147, 103, 16, 50, 38, 221

34, 212, 157, 115, 66, 9, 194, 177, 208, 121, 80, 143, 101, 30, 48

22, 55, 36, 219, 164, 117, 73, 1, 185, 173, 206, 135, 78, 139, 92

141, 99, 29, 57, 43, 211, 155, 113, 71, 15, 183, 169, 197, 127, 85

134, 87, 148, 91, 20, 53, 41, 225, 153, 109, 62, 7, 190, 171, 204

178, 196, 125, 83, 146, 105, 18, 49, 32, 217, 160, 111, 69, 14, 192

5, 188, 176, 210, 123, 79, 137, 97, 25, 51, 39, 224, 162, 118, 61

116, 75, 3, 184, 167, 202, 130, 81, 144, 104, 27, 58, 31, 215, 158

213, 154, 107, 67, 10, 186, 174, 209, 132, 88, 136, 95, 23, 56, 45

47, 37, 220, 156, 114, 74, 12, 193, 166, 200, 128, 86, 150, 93, 19

100, 21, 54, 44, 222, 163, 106, 65, 8, 191, 180, 198, 124, 77, 142

№ 43 - 16

47, 170, 202, 156, 121, 138, 218, 193, 120, 40, 9, 86, 104, 72, 19

67, 21, 46, 168, 203, 163, 135, 145, 219, 191, 119, 42, 4, 77, 95

76, 93, 68, 28, 60, 175, 204, 161, 134, 147, 214, 182, 110, 37, 6

38, 13, 90, 100, 69, 26, 59, 177, 199, 152, 125, 142, 216, 181, 108

195, 115, 39, 11, 89, 102, 64, 17, 50, 172, 201, 151, 123, 143, 223

144, 221, 194, 117, 34, 2, 80, 97, 66, 16, 48, 173, 208, 165, 130

164, 132, 139, 212, 185, 112, 36, 1, 78, 98, 73, 30, 55, 174, 206

169, 197, 155, 127, 141, 211, 183, 113, 43, 15, 85, 99, 71, 29, 57

20, 52, 171, 196, 153, 128, 148, 225, 190, 114, 41, 14, 87, 94, 62

96, 61, 18, 53, 178, 210, 160, 129, 146, 224, 192, 109, 32, 5, 82

3, 83, 103, 75, 25, 54, 176, 209, 162, 124, 137, 215, 187, 111, 31

118, 45, 10, 84, 101, 74, 27, 49, 167, 200, 157, 126, 136, 213, 188

220, 189, 116, 44, 12, 79, 92, 65, 22, 51, 166, 198, 158, 133, 150

131, 149, 222, 184, 107, 35, 7, 81, 91, 63, 23, 58, 180, 205, 159

207, 154, 122, 140, 217, 186, 106, 33, 8, 88, 105, 70, 24, 56, 179

Рассмотрим круговую диаграмму и четно-нечетную мозаику ИМК № 43 – 6

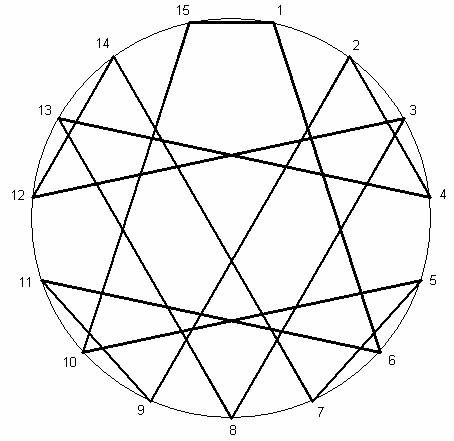
Рис. 22

51	170	138	152	181	202	218	129	120	104	13	26	40	72	79
63	77	46	172	143	159	195	209	223	131	115	102	4	21	35
16	37	68	84	60	179	148	161	190	207	214	126	110	93	2
98	9	30	44	73	86	55	177	139	156	185	198	212	121	112
135	119	103	11	25	42	64	81	50	168	137	151	187	203	219
208	221	130	117	94	6	20	33	62	76	52	173	144	165	194
160	192	199	216	125	108	92	1	22	38	69	90	59	178	146
169	141	155	183	197	211	127	113	99	15	29	43	71	85	57
80	48	167	136	157	188	204	225	134	118	101	10	27	34	66
32	61	82	53	174	150	164	193	206	220	132	109	96	5	18
7	23	39	75	89	58	176	145	162	184	201	215	123	107	91
114	105	14	28	41	70	87	49	171	140	153	182	196	217	128
224	133	116	100	12	19	36	65	78	47	166	142	158	189	210
191	205	222	124	111	95	3	17	31	67	83	54	180	149	163
147	154	186	200	213	122	106	97	8	24	45	74	88	56	175

Рис. 23

Так выглядит один из 1024–х случайно выбранных ИМК15. Если же учесть все схемы расположения чисел 1 , 113 и 225, то всего окажется 1024 · 0,5 (15 – 1) = 7168 различных идеальных магических квадратов 15 х 15 (!) .

Построим еще один интересный ИМК № 43 – 7

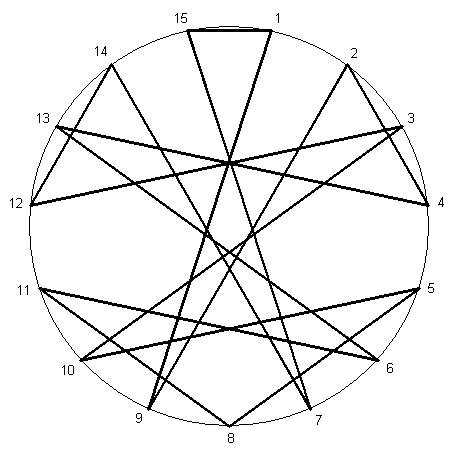
Рис. 24

84	149	95	28	151	42	218	49	120	168	11	182	67	205	126
200	133	76	147	98	19	165	33	221	47	112	175	6	189	74
181	72	203	124	90	138	101	17	157	40	216	54	119	170	13
173	4	195	63	206	122	82	145	96	24	164	35	223	46	117
60	108	176	2	187	70	201	129	89	140	103	16	162	38	214
41	212	52	115	171	9	194	65	208	121	87	143	94	30	153
22	160	36	219	59	110	178	1	192	68	199	135	78	146	92
141	99	29	155	43	211	57	113	169	15	183	71	197	127	85
134	80	148	91	27	158	34	225	48	116	167	7	190	66	204
73	196	132	83	139	105	18	161	32	217	55	111	174	14	185
12	188	64	210	123	86	137	97	25	156	39	224	50	118	166
109	180	3	191	62	202	130	81	144	104	20	163	31	222	53
213	56	107	172	10	186	69	209	125	88	136	102	23	154	45
152	37	220	51	114	179	5	193	61	207	128	79	150	93	26
100	21	159	44	215	58	106	177	8	184	75	198	131	77	142

Рис. 25

Поражает разнообразие мозаичных рисунков.

Поражают безграничные возможности математики.

25 ноября 2007 г. я закончил работу по написанию программы расчета и построению ИМК всех нечетных порядков с 15 по 81 предложенным мною общим методом. Каждый порядок представлен 32-мя наиболее красочными (по мозаике четно-нечетных чисел) идеальными магическими квадратами . Это, во-первых, позволило окончательно утвердиться в универсальности моей модели, а, во-вторых, собрать интереснейший банк идеальных магических квадратов. К сожалению, объем материала таков, что требует издания солидного тома.

27 ноября 2007 г

Москва

Внимание! Магические квадраты – в технике!

http://www.stereo.ru/whatiswhat.php?article_id=254

здесь описывается пример применения МК для жидкокристаллических

экранов телевизора!!!!

“Главной новинкой платформы ЖК-телевизоров Toshiba является алгоритм «магического квадрата». Для гладкой передачи серой шкалы требуется 1024 градации, обеспечиваемые 10-битным преобразованием. Однако в ЖК-панелях используется только 8-битное преобразование, которое обеспечивает всего 256 градаций серого. Для увеличения градаций в панелях Toshiba используется принцип временной модуляции засветки пикселей. Идея основана на способности человеческого глаза интегрально оценивать последовательность коротких вспышек света. Если сначала глаз видит четыре вспышки одного или группы пикселей, затем две и, наконец, одну, то он воспринимает их не раздельно, а как изменение яркости источника. Уменьшение числа импульсов вдвое приводит к кажущемуся двукратному уменьшению яркости. Увеличение градаций серой шкалы с помощью подобного алгоритма происходит благодаря увеличению или уменьшению времени свечения пикселей. Так называемый «магический квадрат» образует группа из 16 пикселей (квадрат 4 на 4), в котором в каждый момент времени (с интервалом 1/60 с для NTSC) зажигается одно и то же число разных пикселей по горизонтали, вертикали и диагонали (см. рис. 1). Благодаря временной модуляции свечения каждого пикселя в этом квадрате алгоритм позволяет учетверить число градаций, подняв их число с восьмибитных 256 до десятибитных 1024. При этом надо еще учесть, что увеличение до 1024 градаций происходит для каждого из первичных цветов (красного, синего и зеленого), что дает в итоге более 1,07 млн. цветов и оттенков. Это обеспечивает плавные цветовые переходы, полностью устраняя видимые границы на больших однотонных полях изображения.”

30	46	56	77	71	45	16	6	22
2	23	35	54	61	78	67	39	10
44	18	7	24	31	48	55	74	68
79	69	40	12	1	20	32	53	63
49	57	73	65	41	17	9	25	33
19	29	50	62	81	70	42	13	3
14	8	27	34	51	58	75	64	38
72	43	15	4	21	28	47	59	80
60	76	66	37	11	5	26	36	52

34	46	20	77	71	45	12	6	58
2	59	35	54	21	78	67	43	10
44	18	3	60	31	52	19	74	68
75	69	40	16	1	56	32	53	27
49	25	73	65	41	17	9	57	33
55	29	50	26	81	66	42	13	7
14	8	63	30	51	22	79	64	38
72	39	15	4	61	28	47	23	80
24	76	70	37	11	5	62	36	48

12	64	58	77	51	45	34	8	20
4	23	15	72	61	80	47	39	28
42	36	7	26	11	66	55	76	50
79	53	38	30	1	22	14	69	63
65	57	73	49	41	33	9	25	17
19	13	68	60	81	52	44	29	3
32	6	27	16	71	56	75	46	40
54	43	35	2	21	10	67	59	78
62	74	48	37	31	5	24	18	70

16	64	22	77	51	45	30	8	56
4	59	15	72	21	80	47	43	28
42	36	3	62	11	70	19	76	50
75	53	38	34	1	58	14	69	27
65	25	73	49	41	33	9	57	17
55	13	68	24	81	48	44	29	7
32	6	63	12	71	20	79	46	40
54	39	35	2	61	10	67	23	78
26	74	52	37	31	5	60	18	66

№	P3	P4	P5	P6	P7	P8	№	P3	P4	P5	P6	P7	P8
1	2	3	4	5	6	7	33	3	4	5	6	7	14
2	2	3	4	5	6	9	34	3	4	5	6	9	14
3	2	3	4	5	7	10	35	3	4	5	7	10	14
4	2	3	4	5	9	10	36	3	4	5	9	10	14
5	2	3	4	6	7	11	37	3	4	6	7	11	14
6	2	3	4	6	9	11	38	3	4	6	9	11	14
7	2	3	4	7	10	11	39	3	4	7	10	11	14
8	2	3	4	9	10	11	40	3	4	9	10	11	14
9	2	3	5	6	7	12	41	3	5	6	7	12	14
10	2	3	5	6	9	12	42	3	5	6	9	12	14
11	2	3	5	7	10	12	43	3	5	7	10	12	14
12	2	3	5	9	10	12	44	3	5	9	10	12	14
13	2	3	6	7	11	12	45	3	6	7	11	12	14
14	2	3	6	9	11	12	46	3	6	9	11	12	14
15	2	3	7	10	11	12	47	3	7	10	11	12	14
16	2	3	9	10	11	12	48	3	9	10	11	12	14
17	2	4	5	6	7	13	49	4	5	6	7	13	14
18	2	4	5	6	9	13	50	4	5	6	9	13	14
19	2	4	5	7	10	13	51	4	5	7	10	13	14
20	2	4	5	9	10	13	52	4	5	9	10	13	14
21	2	4	6	7	11	13	53	4	6	7	11	13	14
22	2	4	6	9	11	13	54	4	6	9	11	13	14
23	2	4	7	10	11	13	55	4	7	10	11	13	14
24	2	4	9	10	11	13	56	4	9	10	11	13	14
25	2	5	6	7	12	13	57	5	6	7	12	13	14
26	2	5	6	9	12	13	58	5	6	9	12	13	14
27	2	5	7	10	12	13	59	5	7	10	12	13	14
28	2	5	9	10	12	13	60	5	9	10	12	13	14
29	2	6	7	11	12	13	61	6	7	11	12	13	14
30	2	6	9	11	12	13	62	6	9	11	12	13	14
31	2	7	10	11	12	13	63	7	10	11	12	13	14
32	2	9	10	11	12	13	64	9	10	11	12	13	14

30	46	56	77	71	45	16	6	22
2	23	35	54	61	78	67	39	10
44	18	7	24	31	48	55	74	68
79	69	40	12	1	20	32	53	63
49	57	73	65	41	17	9	25	33
19	29	50	62	81	70	42	13	3
14	8	27	34	51	58	75	64	38
72	43	15	4	21	28	47	59	80
60	76	66	37	11	5	26	36	52

34	46	20	77	71	45	12	6	58
2	59	35	54	21	78	67	43	10
44	18	3	60	31	52	19	74	68
75	69	40	16	1	56	32	53	27
49	25	73	65	41	17	9	57	33
55	29	50	26	81	66	42	13	7
14	8	63	30	51	22	79	64	38
72	39	15	4	61	28	47	23	80
24	76	70	37	11	5	62	36	48

12	64	58	77	51	45	34	8	20
4	23	15	72	61	80	47	39	28
42	36	7	26	11	66	55	76	50
79	53	38	30	1	22	14	69	63
65	57	73	49	41	33	9	25	17
19	13	68	60	81	52	44	29	3
32	6	27	16	71	56	75	46	40
54	43	35	2	21	10	67	59	78
62	74	48	37	31	5	24	18	70

16	64	22	77	51	45	30	8	56
4	59	15	72	21	80	47	43	28
42	36	3	62	11	70	19	76	50
75	53	38	34	1	58	14	69	27
65	25	73	49	41	33	9	57	17
55	13	68	24	81	48	44	29	7
32	6	63	12	71	20	79	46	40
54	39	35	2	61	10	67	23	78
26	74	52	37	31	5	60	18	66

№	P3	P4	P5	P6	P7	P8	№	P3	P4	P5	P6	P7	P8
1	2	3	4	5	6	7	33	3	4	5	6	7	14
2	2	3	4	5	6	9	34	3	4	5	6	9	14
3	2	3	4	5	7	10	35	3	4	5	7	10	14
4	2	3	4	5	9	10	36	3	4	5	9	10	14
5	2	3	4	6	7	11	37	3	4	6	7	11	14
6	2	3	4	6	9	11	38	3	4	6	9	11	14
7	2	3	4	7	10	11	39	3	4	7	10	11	14
8	2	3	4	9	10	11	40	3	4	9	10	11	14
9	2	3	5	6	7	12	41	3	5	6	7	12	14
10	2	3	5	6	9	12	42	3	5	6	9	12	14
11	2	3	5	7	10	12	43	3	5	7	10	12	14
12	2	3	5	9	10	12	44	3	5	9	10	12	14
13	2	3	6	7	11	12	45	3	6	7	11	12	14
14	2	3	6	9	11	12	46	3	6	9	11	12	14
15	2	3	7	10	11	12	47	3	7	10	11	12	14
16	2	3	9	10	11	12	48	3	9	10	11	12	14
17	2	4	5	6	7	13	49	4	5	6	7	13	14
18	2	4	5	6	9	13	50	4	5	6	9	13	14
19	2	4	5	7	10	13	51	4	5	7	10	13	14
20	2	4	5	9	10	13	52	4	5	9	10	13	14
21	2	4	6	7	11	13	53	4	6	7	11	13	14
22	2	4	6	9	11	13	54	4	6	9	11	13	14
23	2	4	7	10	11	13	55	4	7	10	11	13	14
24	2	4	9	10	11	13	56	4	9	10	11	13	14
25	2	5	6	7	12	13	57	5	6	7	12	13	14
26	2	5	6	9	12	13	58	5	6	9	12	13	14
27	2	5	7	10	12	13	59	5	7	10	12	13	14
28	2	5	9	10	12	13	60	5	9	10	12	13	14
29	2	6	7	11	12	13	61	6	7	11	12	13	14
30	2	6	9	11	12	13	62	6	9	11	12	13	14
31	2	7	10	11	12	13	63	7	10	11	12	13	14
32	2	9	10	11	12	13	64	9	10	11	12	13	14

30	46	56	77	71	45	16	6	22
2	23	35	54	61	78	67	39	10
44	18	7	24	31	48	55	74	68
79	69	40	12	1	20	32	53	63
49	57	73	65	41	17	9	25	33
19	29	50	62	81	70	42	13	3
14	8	27	34	51	58	75	64	38
72	43	15	4	21	28	47	59	80
60	76	66	37	11	5	26	36	52

34	46	20	77	71	45	12	6	58
2	59	35	54	21	78	67	43	10
44	18	3	60	31	52	19	74	68
75	69	40	16	1	56	32	53	27
49	25	73	65	41	17	9	57	33
55	29	50	26	81	66	42	13	7
14	8	63	30	51	22	79	64	38
72	39	15	4	61	28	47	23	80
24	76	70	37	11	5	62	36	48

12	64	58	77	51	45	34	8	20
4	23	15	72	61	80	47	39	28
42	36	7	26	11	66	55	76	50
79	53	38	30	1	22	14	69	63
65	57	73	49	41	33	9	25	17
19	13	68	60	81	52	44	29	3
32	6	27	16	71	56	75	46	40
54	43	35	2	21	10	67	59	78
62	74	48	37	31	5	24	18	70

16	64	22	77	51	45	30	8	56
4	59	15	72	21	80	47	43	28
42	36	3	62	11	70	19	76	50
75	53	38	34	1	58	14	69	27
65	25	73	49	41	33	9	57	17
55	13	68	24	81	48	44	29	7
32	6	63	12	71	20	79	46	40
54	39	35	2	61	10	67	23	78
26	74	52	37	31	5	60	18	66

№	P3	P4	P5	P6	P7	P8	№	P3	P4	P5	P6	P7	P8
1	2	3	4	5	6	7	33	3	4	5	6	7	14
2	2	3	4	5	6	9	34	3	4	5	6	9	14
3	2	3	4	5	7	10	35	3	4	5	7	10	14
4	2	3	4	5	9	10	36	3	4	5	9	10	14
5	2	3	4	6	7	11	37	3	4	6	7	11	14
6	2	3	4	6	9	11	38	3	4	6	9	11	14
7	2	3	4	7	10	11	39	3	4	7	10	11	14
8	2	3	4	9	10	11	40	3	4	9	10	11	14
9	2	3	5	6	7	12	41	3	5	6	7	12	14
10	2	3	5	6	9	12	42	3	5	6	9	12	14
11	2	3	5	7	10	12	43	3	5	7	10	12	14
12	2	3	5	9	10	12	44	3	5	9	10	12	14
13	2	3	6	7	11	12	45	3	6	7	11	12	14
14	2	3	6	9	11	12	46	3	6	9	11	12	14
15	2	3	7	10	11	12	47	3	7	10	11	12	14
16	2	3	9	10	11	12	48	3	9	10	11	12	14
17	2	4	5	6	7	13	49	4	5	6	7	13	14
18	2	4	5	6	9	13	50	4	5	6	9	13	14
19	2	4	5	7	10	13	51	4	5	7	10	13	14
20	2	4	5	9	10	13	52	4	5	9	10	13	14
21	2	4	6	7	11	13	53	4	6	7	11	13	14
22	2	4	6	9	11	13	54	4	6	9	11	13	14
23	2	4	7	10	11	13	55	4	7	10	11	13	14
24	2	4	9	10	11	13	56	4	9	10	11	13	14
25	2	5	6	7	12	13	57	5	6	7	12	13	14
26	2	5	6	9	12	13	58	5	6	9	12	13	14
27	2	5	7	10	12	13	59	5	7	10	12	13	14
28	2	5	9	10	12	13	60	5	9	10	12	13	14
29	2	6	7	11	12	13	61	6	7	11	12	13	14
30	2	6	9	11	12	13	62	6	9	11	12	13	14
31	2	7	10	11	12	13	63	7	10	11	12	13	14
32	2	9	10	11	12	13	64	9	10	11	12	13	14