Георгий
Александров
О ЧИСЛЕ ПАНДИАГОНАЛЬНЫХ КВАДРАТОВ 4x4
Известно, что число пандиагональных квадратов
равно 48 (без учета поворотов и
отражений). Если же принять во внимание преобразования, связанные с торическими переносами, то в итоге будем иметь всего три
вида пандиагональных
квадратов ( см. «Википедию»,
статья «Магический квадрат», раздел «Дьявольский магический квадрат»).
Но внимательно
проанализируем эти три варианта ( см. плакат по
ссылке
http://renuar911.narod.ru/Diablo.jpg ).
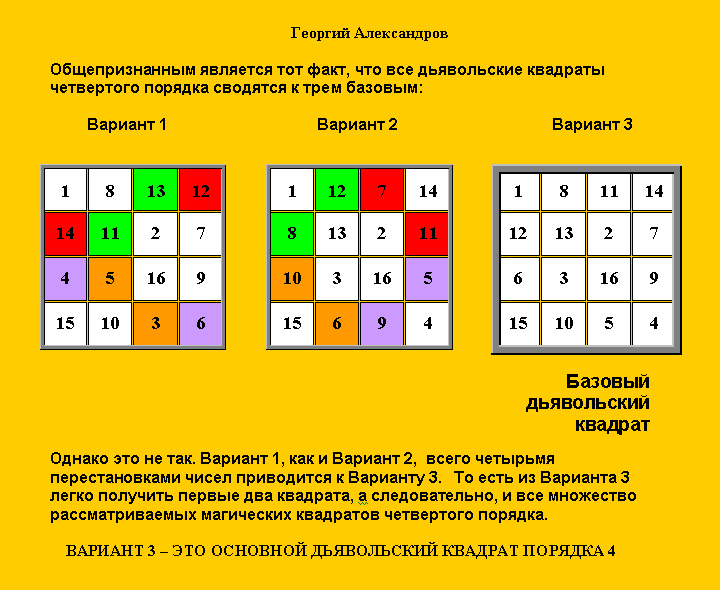
Если в первом варианте поменять местами ячейки, окрашенные в одинаковый
цвет, то получим в точности Вариант 3. То же самое и для варианта 2: обмен
ячейками дает тот же, третий вариант. Отсюда закономерный вывод: достаточно
иметь один базовый пандиагональный квадрат 4 x 4 и из него, посредством самых
различных и довольно простых перестановок, можно найти абсолютно все компоновки
ячеек.
* * *
В качестве рабочей
гипотезы я предполагаю, что для любой матрицы
n x n существует единственный базовый
идеальный магический квадрат,
допускающий различные перестановки как групп
ячеек, так и отдельных клеток, вследствие чего набирается весь спектр идеальных
и пандиагональных квадратов.
Если такая гипотеза
верна, то отпадет необходимость рассчитывать астрономическое число вариантов
всех магических квадратов.
Вообще-то мое мнение
таково: по-настоящему магическим квадратом нечетного порядка должен
называться идеальный магический квадрат, то есть одновременно пандиагональный и ассоциативный. Поиск базового идеального квадрата - важнейшей этап решения рассматриваемой
проблемы.
В
качестве идеального магического квадрата порядка n = 4k наверное следует принимать базовый пандиагональный квадрат.
Для нечетно-четных
магических квадратов дело обстоит сложнее. Скорее всего, базовый магический
квадрат должен быть привязанным к базовому идеальному квадрату порядка n/2. Но это пока это мои предположения и вопрос
остается открытым.
20 октября
Москва