Глава 8. В которой  мы с  Андрюшей

решаем графически задачу Арнольда

 о двух старушках

 

Совсем недавно, 3 июня 2010 года, из Парижа пришло печальное известие: ушел из жизни великий российский математик Владимир Игоревич Арнольд. Он был учеником А.Н.Колмогорова, был ученым, решившим в 1957 году тринадцатую проблему Гильберта. То есть показал, что любая непрерывная функция нескольких переменных может быть представлена в виде комбинации конечного числа функций от двух переменных. Его публикации представляли собой всегда свежий и обычно геометрический подход к традиционным разделам математики.

- Деда! Какую книгу написал он?

- Я, Андрюшенька, очень люблю его интересный сборник «Задачи для детей от 5 до 15 лет». Ну, прямо для тебя, мой родной! В Интернете его можно посмотреть по ссылке  http://ilib.mirror1.mccme.ru/pdf/VIA-taskbook.pdf . Вот начало текста:

 

 

Попробуем начать именно с этих задач?

- Давай. Начинаем с первой:

 

“1. У Маши не хватало для покупки букваря семи копеек, а у Миши одной копейки.  Они сложились, чтобы купить один букварь на двоих,  но денег все равно не хватило. Сколько стоил букварь?”

 

- Итак, ученик ты мой, начинай рассуждать.

- Одну секунду, деда. Пусть у Маши была одна копейка. Значит, букварь должен стоить восемь копеек. Тогда у Миши было бы семь копеек. Так? Если одну копейку Маши сложить с семью копейками Миши, то будет восемь копеек,  и они бы купили букварь. Но поскольку на самом деле денег им не хватило, то у Маши денег вообще не было, а  Букварь бы стоил семь копеек. У Миши, значит,  было шесть копеек. Ноль плюс шесть – денег бы не хватило. Букварь, следовательно, стоил семь копеек. Верно?

- Правдоподобно, Андрюша! Тут ответов нет? Эх, нет. Пока что не вижу никаких противоречий. Значит, решение верное. Давай третью задачу попробуй:

 

“3. Кирпич весит фунт и полкирпича. Сколько фунтов весит кирпич?”

 

- Деда, а что такое фунт?

- Фунт это английская мера веса. У нас вес измеряют в килограммах. Ты это знаешь. Так вот, один фунт – это чуть меньше полкило.

- Ясно, дедуля. Тогда решаю. Если кирпич весит фунт и полкирпича, то он весит фунт и фунт, то есть два фунта. То есть чуть меньше килограмма.

- Ну, если ты прав, то странно. Я ведь по образованию строитель и знаю, что обычный красный кирпич весит три килограмма. Что-то мелкий кирпич получается у Арнольда.

- Наверное, это детский кирпичик.

- Остряк, однако! Ладно, задача тринадцать:

 

“13. На книжной полке рядом стоят два тома Пушкина: первый и второй. Страницы каждого тома имеют вместе толщину 2 см, а обложка – каждая – 2 мм. Червь прогрыз (перпендикулярно страницам) от первой страницы первого тома до последней страницы второго тома. Какой путь он прогрыз? ”

 

- Если книги стоят правильно и сначала первый том, а за ним второй, и при этом корешки смотрят на нас, то червяку достаточно прогрызть переднюю обложку первого тома и заднюю обложку второго тома, то есть 4 миллиметра.

- Погоди, Андрюш, что-то я не понимаю. Ты сделай рисунок.

- Ну вот, посмотри. Кружочками я обвел первый и второй тома. Если корешки томов смотрят в нашу сторону, то первая страница первого тома справа, а последняя страница, допустим сотая, будет слева. Также и у второго тома. Червяку нужно с первой страницы первого тома попасть на сотую страницу второго тома. Я это и показал линией с точками на концах. Всего-то червю прогрызть достаточно две обложки. Ведь верно?

 

 

 

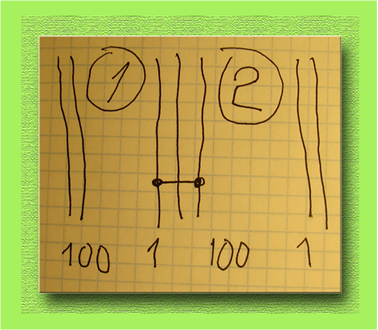
- Ну, ты даешь, Андрюша! Я бы в жизни не догадался!

- Дедуль! А  вот задача про старушек, о которых ты мне говорил! Посмотри – задача номер пять.

- Ой, и верно. Мне казалось, эта задача где-то в середине сборника. Давай ее решать. Итак, условие:

 

 

 

- Деда! Что-то сложно для меня. Никак ее не могу понять. Ты поясни поясней.

- Давай сделаем чертеж. Тогда и мне все станет ясно. Построения производим аккуратно и наглядно:

 

 

- Деда! Мне не все понятно. Откуда взялись числа 21, 16, 12, 1 ?  Их в задаче не было!

- Андрюша! Ты же прекрасно знаешь, что девять часов вечера – это 21 час, 4 часа после обеда – это 16, полдень – это 12 часов. Единицей же я обозначил расстояние между пунктами А и В. Мог принять и 2, и 3, и просто L… Сколько угодно, так как определять в задаче данное расстояние не требуют. Первая старушка пришла в пункт В в 16 часов. Для общности я и обозначил    .  Вторая старушка пришла в пункт A в 21 час, и поэтому   . Время   – это время встречи двух старушек. Найти же нужно время восхода солнца   , когда старушки одновременно вышли из пунктов. А чтобы время восхода найти, нужно определить время  . На рисунке я для упрощения обозначил интервалы времени и расстояний. Чтобы успешно решить задачу, приходится анализировать подобные треугольники. Каждую пару подобных треугольников я закрасил одним цветом. И вот что вытекает из подобия:

 

 

 

Если избавиться от знаменателя, то эта система будет выглядеть еще проще:

 

 

Наша главная задача – найти именно  t . Из первого уравнения выражаем  x :

 

 

Из второго можно выудить   :

 

Подставляем в него найденный    :

 

 

Отсюда уже легко найти нужное   :

 

Поскольку нас интересует только положительное значение времени  t , то окончательно:

 

  часов.

 

То есть, Андрюшенька, рассвет в тот день наступил в :

 

  часов

 

- Так это все? Задача решена?

- Да, решена полностью. Погоди, - у меня есть идея! Давай мы эту задачу попробуем решить чисто графически.

- Деда, но ты же построил график и он нам очень помог.

- Он нам помог выполнить аналитическое решение. Главное, что мы с тобой выяснили – параметр t  определяется, как среднее геометрическое. А я знаю целых два метода построения среднего геометрического при помощи циркуля и линейки. Поэтому данную задачу можно решать вообще без вычислений, а только путем построения линий и окружностей.

- Ой, как интересно! Давай я принесу свой альбом для рисования. Там хорошая, плотная бумага. А циркуль у нас есть?

- Да, есть. Я недавно видел его в ящике для инструментов. Он, кажется, рядом с молотком лежит.

- Я сейчас найду его, дедуль!

- Ну, дерзай, если я не ошибся.

- Вот он! Там и карандаш был, а линейка на моем столике.

- Какой же умник, Андрюша! Я тобой восхищаюсь. Ну, что ж, теперь обдумаем стратегию графического решения. У меня где-то в Интернете статья лежит. Там как раз этот вопрос подробно освещен. Подожди пять минут…  Вот, статья Бориса Якубовского. Там прекрасные рисунки, которые я сделал по его просьбе.

- Деда, кто такой Якубовский?

- Его зовут Борис Андреевич. Я с ним впервые познакомился в Аргентине. Он приезжал к своему отцу Андрею Борисовичу Якубовскому, с которым я до сих пор дружу. А там мы играли с Борисом в теннис. После он стал большим бизнесменом и по чудесному стечению обстоятельств недалеко от нас купил участок и построил очень хороший дом. Помнишь, мы с тобой на велосипеде проезжали по большой улице, и я показал тебе калитку?

- Ты мне сказал, что там живет дядя Боря, да?

- Да, точно. Это было в июне, когда мы чуть в грозу не попали. Но успели. Только вошли в дом и вдруг как громыхнет! А ливень-то какой был!... Ой, закончим отвлекаться. Вот, нашел! Статью все-таки обнаружил по ключевым словам. Молодец  гугл!  - не подкачал. Этот рисунок взят из Википедии:

 

 

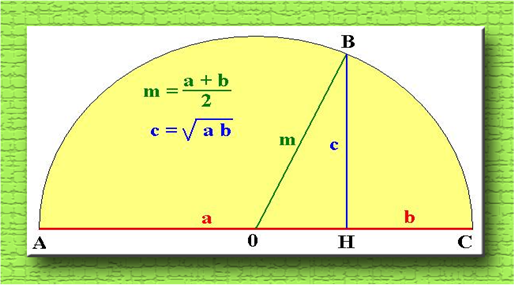
Даны отрезки AH = a  и  HC = b . Нужно построить отрезок прямой, равный среднему геометрическому отрезков   a  и   b.  Если суммарный отрезок  AC = a + b  поделить пополам при помощи циркуля и линейки (помнишь, я тебе подробно объяснил этот красивый метод), то получим точку  O . Примем эту точку за центр окружности с радиусом, равным  AO  или  OC и проведем полуокружность. Из точки  H  восстановим перпендикуляр (ты это тоже должен помнить, Андрюша!) до пересечения с окружностью. Обозначим эту точку через  B .  Синий отрезок HB  и будет средним геометрическим отрезков  a  и  b .

- Деда! Тогда зеленая прямая, это что?

- Это, Андрюша, среднее арифметическое. Вычисляется по зеленой формуле. Но кроме этой простой схемы построения есть менее известная и более сложная. Тут нужны знания такой науки, как тригонометрия. Но сейчас поверь мне просто на слово. Вот рисунок:

 

 

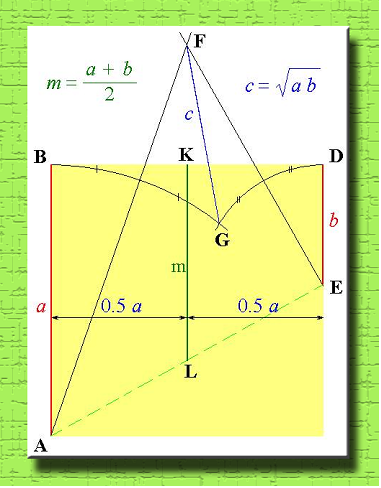
Желтый прямоугольник – это квадрат со стороной  a . Видишь, как теперь расположены отрезки  a   и  b?  Не последовательно, как в предыдущем случае, а параллельно. Проводим дуги циркулем из точек A  и  E до их пересечения  (точка  G ). Каждую дугу делим пополам. Я тебе рассказывал, как делить дугу окружности – точно так же, как отрезок прямой. Проводим линии AF  и  EF . Так вот, отрезок  FG  будет средним геометрическим отрезков  a   и  b .

- Вот это да, дедуля! Ни за что не стал бы такую громоздкость чертить.

- Зато интересно! Недаром алгебра и геометрия считаются удивительными науками. Итак, теперь применим наши познания для решения задачи о двух старушках. Сейчас я тебя отпускаю отдыхать, а сам помозгую над рисунками. Хорошо?

- Ладно! Я посмотрю мультик “Сам-Сам” и съем бананчик…

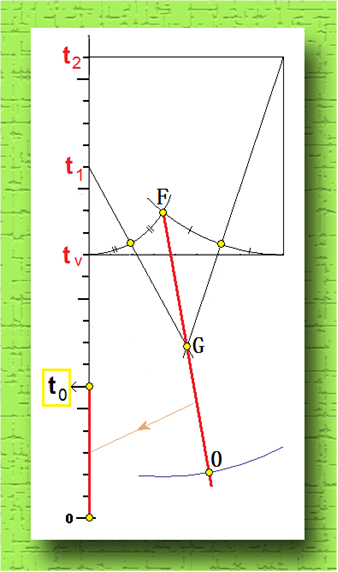
- Андрюша! Все, уже построил! Иди, погляди на картинки. Вот у нас вертикальная временная ось.

 

 

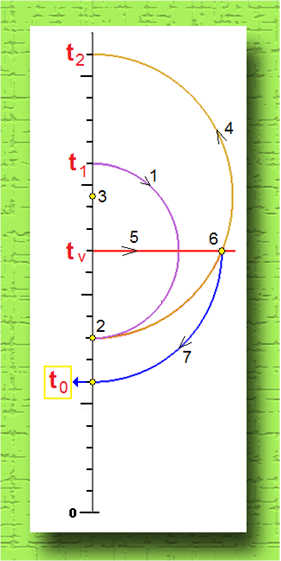
Сначала ножку циркуля ставим в точку места встречи     и радиусом     строим полуокружность в направлении стрелки 1. Получаем на оси точку 2.  Далее строим точку 3. Она – середина отрезка, ограниченного точкой 2 и   . Ты ведь знаешь, как при помощи циркуля и линейки делить отрезок пополам. В точку 3 ставим ножку циркуля и, понятно каким радиусом,  чертим полуокружность  4 . Из точки    строим перпендикулярную линию 5 .  Мы вчера с тобой строили перпендикуляры при помощи опять же циркуля и линейки. Пересечение полуокружности 4 и перпендикуляра 5 дает нам точку 6.  Второй раз ставим иглу циркуля в точку    и опять, -  понятно каким радиусом, - чертим четверть окружности синего цвета. Пересечение с осью времени дает значение    - это время восхода солнца.

- Дедуля, а перпендикуляр и есть среднее геометрическое отрезков?

- Совершенно верно. Все, как в рисунке из Википедии. Ну, а второй рисунок я доверяю  тебе самостоятельно изучить. Он несложный. Скажу только, что начинать надо с построения квадрата. А как строить квадрат, мы с тобой уже знаем.

- Хорошо, деда! Сейчас начну изучать.

 

 

Скажи, вот, а сторона квадрата равна  минус    ?

- Совершенно верно.  Это самый главный элемент построения.

- Все понял, деда! Завтра я попробую найти время восхода при других старушках.

- Каких это других?

- Ну, более шустрых. Которые не так долго ходят. Это ж вредно, правда?

 

 

6  марта 2011