Глава 12. В которой  внук и я рассуждаем

о физическом явлении,

подтвержденном математически

 

- А теперь, Андрюшенька, поговорим о пользе математики. Я тебе  упомянул однажды, как мы выпиливали из фанеры прямоугольный треугольник, который предварительно начертили с использованием замечательной формулы Пифагора. Но вот расскажу про один случай, который надолго врезался мне в память.

- Как это врезался? Прямо в голову? Помнишь, мы с тобой кидали друг другу летающую тарелку, - так она однажды как в лоб мне врезалась. Я даже заплакал.

- Я в смысле, что надолго тот случай запомнился. Даже сейчас, по прошествии  шести лет, все вижу до мельчайших деталей.

- Ой, что же это был за случай?  Расскажи, пожалуйста!

- Дело было так. Я увлекался волнами на воде. Но не на море или озере, а в специальном стеклянном лотке. Представь себе прямоугольный лоток,  о котором мы говорили в Главе 9,  но его стенки выполнены не из железа, а из оконного стекла. Он длинный-предлинный, аж двадцать метров! Торцы его замурованы деревянными щитами и в него до двух третей высоты бортов налита вода. Но и это не все. Я сделал два пересекающихся лотка.

- Как это понять?

- А вот взгляни на чертеж.

 

 

 

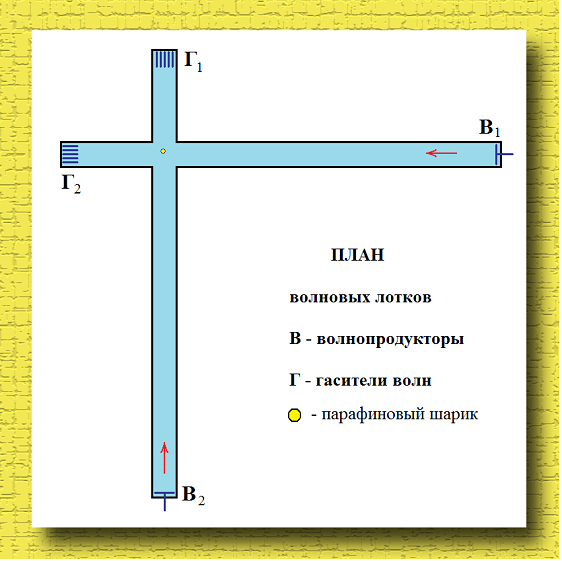
Это я изобразил лотки, если на них смотреть сверху. Лотки  расположены  под углом  90 градусов друг к другу. В начале лотков имеются волнопродукторы,  которые я обозначил буквой  В  с индексами один и два.

- Для чего нужны эти продукторы?

- Волнопродукторы?! Они нужны для того, чтобы в лотках создавать волны нужной длины и высоты.

- А как они, дедуля, это делают? И как они выглядят?

- Ну, представь себе дверь, у которой петли не сбоку, а внизу. И ты ее берешь рукой, ставишь вертикально и начинаешь  потом качать туда-сюда, как маятник. Если такая дверь будет в воде, то от нее пойдут волны. Но в моем случае эту дверь двигала не рука, а специальный шатун, соединенный с электромотором.

- Это как колеса у паровоза, да?

- Примерно так, хотя конструкция механизма иная и попроще. Но не буду вдаваться в такие механические детали… Это ты в пятитомнике Артоболевского посмотри. Вон на полке, в коричневых переплетах.  Ну, так вот. Сделал я эти два сходящихся лотка  с определенной целью. Если поместить в область пересечения лотков парафиновый шарик, и гнать в обоих лотках волны, то что будет с этим шариком?

- Что значит, парафиновый?

- Парафин, Андрюша, - это из чего свечи делают. Плотность парафина близка к плотности воды и можно так отрегулировать вес шарика, чтобы он не плавал и не лежал на дне, а находился в толще воды, как рыба.

- Деда, разве в толще воды тоже гуляют волны?

- Да, внучек, при волнении все частички жидкости приходят в движение, которое, правда, убывает с глубиной. Так вот, я продолжаю свой рассказ.  Если посмотреть на один из лотков сбоку, то можно увидеть очень красивое движение воды, похожее на синусоиду.

 

 

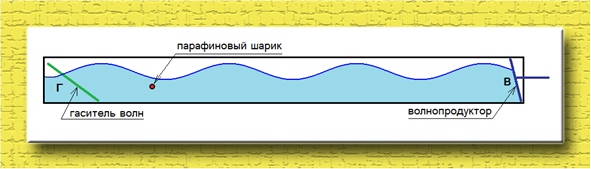
- Деда, а что это за гаситель волн?

- Если волну в конце не гасить, то она отразиться от левого торца лотка и будет накладываться на основную. Синусоидальность всей картины сразу испортится. Этого надо избегать. Гаситель волн прост до невозможности: я кладу связки прутьев и травы. Бегущая волна попадает в поры этого своеобразного веника и эффективно дробится почти полностью. Далее, я прикрепил прямо над шариком цифровой фотоаппарат и в режиме видео снимал процесс движения этого шарика при одинаковых и различных волнах в лотках. При одинаковых волнах траектория шарика была близкой к круговой. Это четко было видно, если рассматривать видеофильм по кадрам.  Положение шарика на каждом кадре я обозначал кружком и последовательно чертил между ними прямые линии синего цвета.

А  вот  если волны оказывались немного разными, то происходило нечто неожиданное. Это нечто запечатлено на рисунке:

 

 

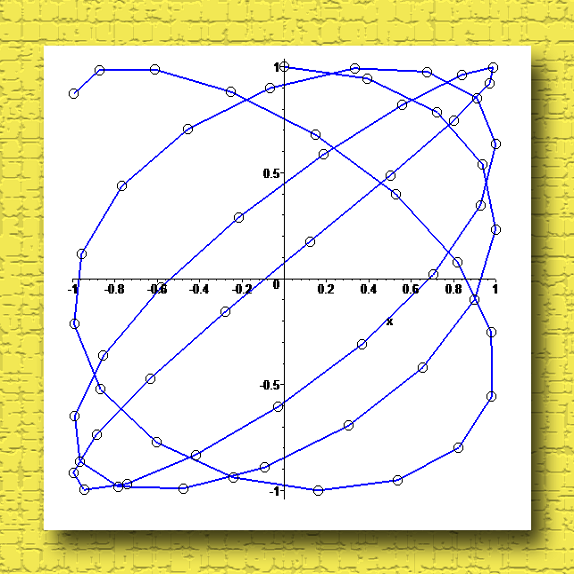
Рис. A

 

Начало движения шарика идет от верхней единички. Сначала по часовой стрелке шарик по некой спирали, но на третьем обороте, вдруг, разворачивается и продолжает двигаться уже в противоположную сторону!

- Как это? Почему так происходит, дедуля?

- Я сначала подумал, что это некая случайная ошибка эксперимента. Мало ли что может мешать чистоте опыта. Неравномерность движения волнопродуктора  или, например, недостаточно эффективная работа гасителей волн. Или же шероховатость внутри лотка. Причин тысяча. Но я решил проверить все математически.

- Как же математически описать лоток с волнами?

- Весь лоток с водой, шариками и прочими делами, конечно же, никакая математика не опишет. Математика может лишь проверить гипотезу,  в соответствии с которой шарик совершает траекторию,  выраженную  через такие тригонометрические функции,  как синус и косинус.

- А откуда ты взял, что именно через эти функции,  а не, допустим, через тангенс и котангенс? А вдруг даже не через тригонометрию, а через логарифм какой-нибудь или полином?

- Ну, кое-какие предварительные знания я имею. Ведь не зря тебе говорил, что если волны одинаковые в обоих лотках, то шарик движется почти по кругу. Как ты думаешь, каким уравнением это можно описать?

- Не знаю, дедуля. Скорее всего, уравнением окружности. А каким еще?

- В принципе верно. Но не буду тебя мучить, а сам отвечу на вопрос:  

 

 

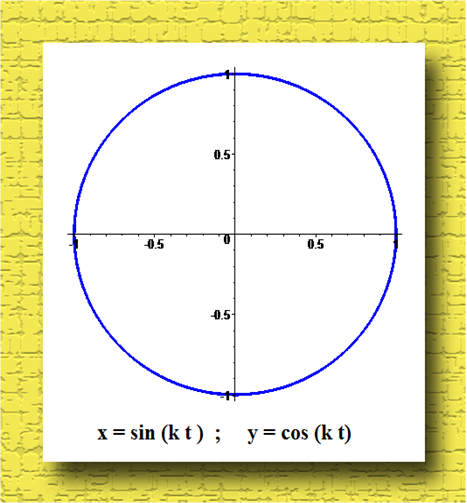
Уравнения показаны в параметрическом виде. Здесь  t  - это параметр, а   k   - любое число. Данный график получается при любом  значении  k . В самом деле, если избавиться от параметра, то придем к уравнению окружности в декартовых координатах:

 

 

- Деда, но у нас же не окружность, а вон какой вихрь образовался! Тут уравнение ого-го какое требуется!

- Попробуем сначала простым параметрическим уравнением аппроксимировать. Вот таким:

 

 

 

Коэффициенты    и    выявим полюбившим нам методом Монте-Карло. Но сначала графически определим координаты кружочков, что на  Рис. A.

- Ой, но их же так много! Целый день придется измерять и записывать.

- Измерять не будем, а просто при помощи курсора в Paint  снимем экранные координаты центров кружочков, а потом с помощью простенькой программы пересчитаем на нужные нам координаты, используя координату пересечения осей 0x  и  0y. Ты пока погуляй, я быстренько сам сделаю эту скучную работу…

 Вот смотри, Андрюшенька, пока ты бегал, я и координаты нашел, и программу составил:

 

open #1,"XYappr.txt","w"

dim t(100),x(100),y(100),t(100)

z=.001

for k=1 to 59:t(k)=k*pi/8:next k

x(1)=0:x(2)=0.39:x(3)=0.72:x(4)=0.94:x(5)=1.0:x(6)=0.9:x(7)=0.66:x(8)=0.31:x(9)=-0.09:x(10)=-0.48:x(11)=-0.79:x(12)=-0.97:x(13)=-0.99:x(14)=-0.85:x(15)=-0.58:x(16)=-0.21:x(17)=0.19:x(18)=0.56:x(19)=0.84:x(20)=0.99:x(21)=0.97:x(22)=0.80:x(23)=0.50:x(24)=0.12:x(25)=-0.28:x(26)=-0.63:x(27)=-0.89:x(28)=-1.0:x(29)=-0.95:x(30)=-0.74:x(31)=-0.42:x(32)=- 0.03:x(33)=0.37:x(34)=0.70:x(35)=0.93:x(36)=1.0:x(37)=0.91:x(38)=0.68:x(39)=0.33:x(40)=-0.07:x(41)=-0.45:x(42)=-0.77:x(43)=-0.96:x(44)=-0.99:x(45)=-0.87:x(46)=-0.60:x(47)=-0.24:x(48)=0.16:x(49)=0.54:x(50)=0.82:x(51)=0.98:x(52)=0.98:x(53)=0.82:x(54)=0.53:x(55)=0.15:x(56)=-0.25:x(57)=-0.61:x(58)=-0.87:x(59)=-0.99

 y(1)=1:y(2)=0.94:y(3)=0.79:y(4)=0.54:y(5)=0.23:y(6)=-0.1:y(7)=-0.42:y(8)=-0.69:y(9)=-0.89:y(10)=-0.99:y(11)=-.98:y(12)=-0.86:y(13)=-0.65:y(14)=-0.36:y(15)=-0.04:y(16)=0.29:y(17)=0.59:y(18)=0.82:y(19)=0.96:y(20)=1.0:y(21)=0.92:y(22)=0.75:y(23)=0.49:y(24)=0.18:y(25)=-0.16:y(26)=-0.47:y(27)=-0.73:y(28)=-0.92:y(29)=-1.0:y(30)=-0.97:y(31)=-0.83:y(32)=-0.60:y(33)=-0.31:y(34)=0.02:y(35)=0.35:y(36)=0.63:y(37)=0.85:y(38)=0.98:y(39)=0.99:y(40)=0.90:y(41)=0.71:y(42)=0.44:y(43)=0.12:y(44)=-0.21:y(45)=-0.52:y(46)=-0.77:y(47)=-0.94:y(48)=-1.0:y(49)=-0.95:y(50)=-0.80:y(51)=-0.56:y(52)=-0.25:y(53)=0.08:y(54)=0.40:y(55)=0.68:y(56)=0.88:y(57)=0.99:y(58)=0.98:y(59)=0.87

a0=1:b0=1:s1=10^5:nn=1000000:for j=1 to nn

a=a0*(1+z*(ran()-.5)):b=b0*(1+z*(ran()-.5))

s=0:for i=1 to 59:t=t(i):x=x(i):y=y(i) :x1=sin(t*a):y1=cos(t*b)

s=s+(x-x1)^2+(y-y1)^2:next i:if s<=s1 then:print a,b,s

print #1, a using "##.######", b using "##.#######", s using "##.######"s1=s

a0=a:b0=b:fi:next j

 

Видишь, у нас пятьдесят девять опорных точек. Теперь запускаем прогу и ждем.

Итог неплохой:

 

 

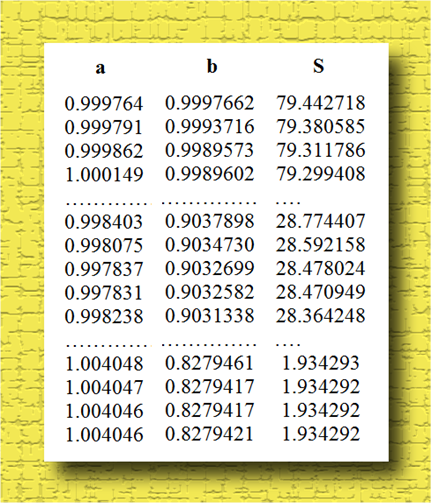
У нас сумма квадратов отклонений не только по игрекам, но и по иксам. Получается, что 118 сумм квадратов отклонений дает 1,934. Это, как мне кажется, совсем приличная сходимость  и аппроксимация должна быть удовлетворительной.  Впрочем, построим  и тогда увидим. Я сейчас составлю программу в Maple:

 

k1:=1.00405;k2:=.827942;plot([sin(t*k1),cos(t*k2),t=0..23.5],thickness=3,color=blue);

 

и наложу затем на полученную кривую экспериментальные точки, построенные при помощи:

 

with(plots):X:=[0,0.39,0.72,0.94,1.0,0.90,0.66,0.31,-0.09,-0.48,-0.79,-0.97,-0.99,-0.85,-0.58,-0.21,0.19,0.56,0.84,0.99,0.97,0.80,0.50,0.12,-0.28,-0.63,-0.89,-1.0,-0.95,-0.74,-0.42,-0.03,0.37,0.70,0.93,1.0,0.91,0.68,0.33,-0.07,-0.45,-0.77,-0.96,-0.99,-0.87,-0.60,-0.24,0.16,0.54,0.82,0.98,0.98,0.82,0.53,0.15,-0.25,-0.61,-0.87,-0.99]: Y:=[1,0.94,0.79,0.54,0.23,-0.098,-0.42,-0.69,-0.89,-0.99,-0.98,-0.86,-0.65,-0.36,-0.04,0.29,0.59,0.82,0.96,1.0,0.92,0.75,0.49,0.18,-0.16,-0.47,-0.73,-0.92,-1.0,-0.97,-0.83,-0.60,-0.31,0.02,0.35,0.63,0.85,0.98,0.99,0.90,0.71,0.44,0.12,-0.21,-0.52,-0.77,-0.94,-1.0,-0.95,-0.80,-0.56,-0.25,0.078,0.40,0.68,0.88,0.99,0.98,0.87]:g:=plot([[X[i],Y[i]]$i=1..59],x=-1..1,style=POINT,symbol=CIRCLE,symbolsize=20,color=black):display(g);

 

 Вот что в итоге:

 

 

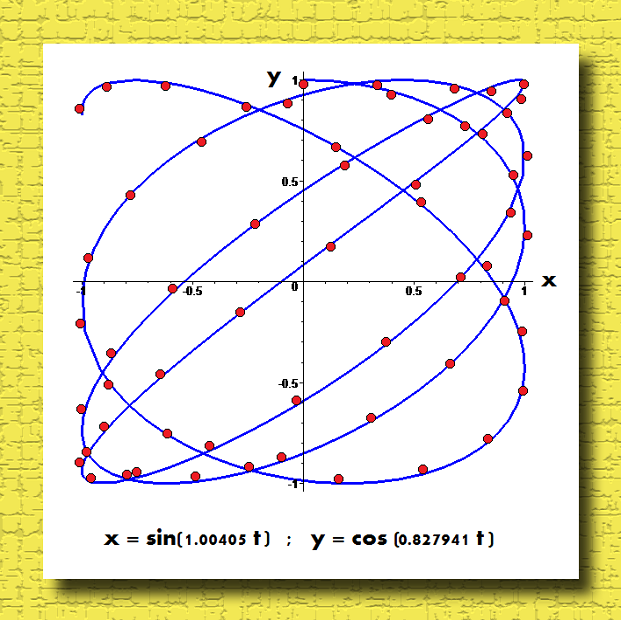
- О! Дедуля! Это ж просто идеальное совпадение! И даже разворот совпал полностью!

- К сожалению, внучек, подобные удачи крайне редки в науке. Все зависит от чистоты эксперимента  и  правильно выбранной гипотезы.

 

 

13  апреля  2011