Георгий Александров
Идеальный совершенный магический квадрат
четного порядка
Идеальный магический квадрат – это матрица n
x n , заполненная
неповторяющимися числами таким образом, что, во-первых, сумма в каждой строке,
каждом столбце, в каждой главной диагонали и в каждой ломаной диагонали равны магической константе, и, во-вторых,
сумма любой пары центрально симметричных ячеек равна одному и тому же числу.
Для матриц n x
n , у которых n=2k+1 и n=4k,
где k=2,3,4,… , удается
скомпоновать идеальный магический квадрат, заполненный всеми числами от 1 до n2 . При n=4k+2,
где k=1, 2, 3, …,
идеальные квадраты существуют, но числа в них не являются частью
начального натурального ряда. То есть данные идеальные магические квадраты могут
быть только нетрадиционными. Пока еще не найдены идеальные магические
квадраты 3 х
3 и 4 х 4 .
Идеальные магические
квадраты проще всего строить при помощи латинских квадратов. Целью настоящей
статьи является выявление наиболее простых и универсальных латинских квадратов,
отталкиваясь от которого легко бы находились идеальные магические квадраты
любого четного порядка.
1.
Идеальные совершенные нетрадиционные
магические квадраты
порядка n = 4k + 2
От
моего коллеги Н. Макаровой я узнал, что существует метод построения квадрата порядка 6, который описан в журнале "Наука
и жизнь", № 5,
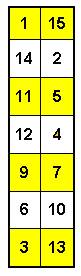
Рис. 1. Решение Н.Макаровой
Разными
цветами выделены четные и нечетные числа.
Латинский
квадрат в данном случае очень легко достраивается (Рис. 2):
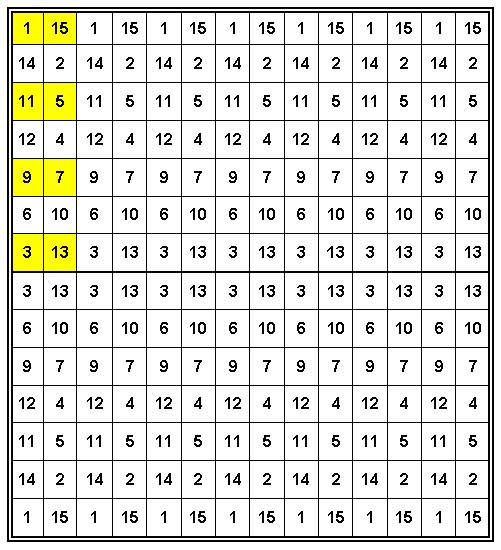
Рис. 2 . Латинский квадрат Н.Макаровой
Пусть числа в ячейках –
это Z( i, j ) , а Zmax – наибольшее число в поле латинского
квадрата. Тогда идеальный нетрадиционный магический квадрат M(i,j) строится согласно правилу:
M(
i,j ) = Zmax [Z(
i, j ) – 1
] +
Z( j, i)
Допустим,
начало координат находится в левом верхнем углу. Параметр i – номер строки , j – номер столбца. В нашем
примере Zmax = 15. При i =2 j =
3 Z( 2 , 3 ) = 14 ; Z( 3 , 2) = 5. Следовательно, M( 2 , 3 ) = 15 ( 14 – 1 )
+ 5 = 200 . Вычислив таким образом все M( i,j ), получим решение
(Рис. 3):
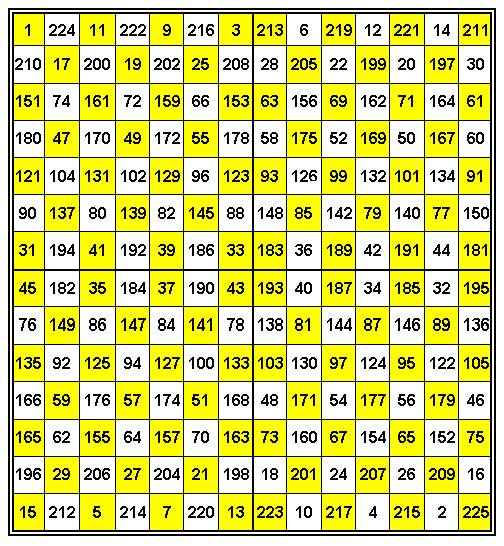
Рис. 3. Идеальный нетрадиционный
совершенный магический квадрат Н.Макаровой.
Моя техника вычислений несколько отличается от той, которой пользуется Н.Макарова, но результат получается абсолютно одинаковый ( см. http://www.natalimak1.narod.ru/netradic.htm , рис. 32)
Первое, на что я обратил внимание, - это
отсутствие какой-либо явной закономерности в расстановке чисел на Рис.1. На числовые
последовательности у меня особое чутье, ибо
гляжу на них, как шахматист смотрит на расстановку фигур в процессе игры
и просчитывает возможные ходы. Это происходит на уровне подсознания и в довольно
быстром темпе. Попытаюсь подробно описать
ходы моих рассуждений.
Глядя на рисунок 1, появляется ощущение дискомфорта, и возникают
вопросы. Я мысленно говорю себе: ”Ну хорошо, пары
четных и нечетных чисел регулярно чередуются. Но почему нечетные числа в левой
колонке идут в последовательности 1 11
9 3 , а в
правой – 15 5
7 13 ? Абсолютные
разницы между соседними числами восхищения тоже не вызывают: 10
2 6 . У четных чисел тенденции не более
логичные ( в левой колонке 14
12 6 , в правой -
2 4 10 ),
при этом разницы: 2 и 6 . Получается, что прекрасный магический
квадрат на Рис. 3 (идеальный и совершенный)
вытекает из неясной последовательности четных и нечетных чисел.
Это кажется мне странным”.
Далее формируются более конструктивные мысли: “На
Рис. 3 показан четно-нечетный узор нетрадиционного идеального магического
квадрата. Видно, что желтые ячейки с нечетными числами максимально распылены по
всей матрице. Возникает подозрение: быть может, сильное распыление есть
результат неудачного сочетания чисел в полустолбцах? Тогда можно попытаться кинуться
в другую крайность – то есть получить
узор в матрице, при котором четные и нечетные числа группировались бы в крупные
блоки с соблюдением незыблемого правила: по всем 4n направлениям (по
строкам, столбцам, главным и ломаным диагоналям) количество желтых ячеек должно быть четным. В голове возникают две
картинки, которые я года три-четыре назад досконально изучал при решении
несколько иной задачи (см. Рис. 4):
a) b)
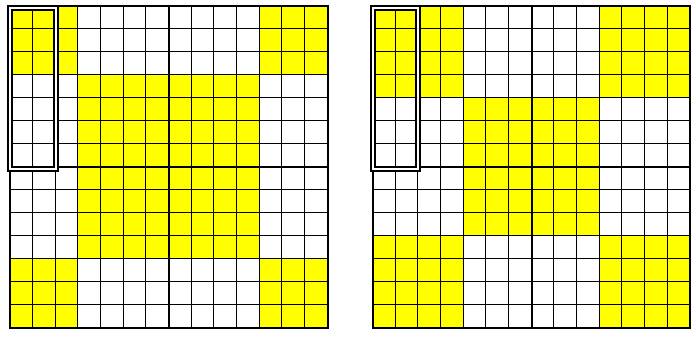
Рис. 4. Возможные схемы
расположения четных и нечетных чисел.
Какая из этих схем более предпочтительна? Выделяю в каждой матрице два полустолбца.
Важно отметить, что тут нет никакой серьезной
науки. На данные действия меня толкают ассоциации. Почему они такие – я сам
толком не понимаю.
В первом случае сначала идут три пары нечетных
чисел и затем четыре пары четных. Во втором – наоборот. Что же принять? “.
Когда при решении математической задачи
оказывается избыток неизвестных параметров, обычно ищут дополнительные
уравнения. Точно так же и я вынужден искать дополнительную цепочку логических
выводов.
На помощь привлекаю следующую последовательность
рассуждений: “Идеальных магических квадратов порядка 4k+2 не существует. Это
доказано математиками прошлого и позапрошлого веков. Можно построить только
нетрадиционные идеальные квадраты, у которых максимальное число в ячейке
определяется выражением (n + m)2,
где m = 1, 3,
5, … . Параметр m
довольно
интересный: при одних его значениях нетрадиционные магические квадраты не
строятся вообще, при других строятся, но
с дублированием некоторых чисел. Для того, чтобы найти
m, при котором нетрадиционный идеальный магический квадрат
получался бы полноценным, приходится делать изнурительные комбинаторные
расчеты. С увеличением порядка n усложняется и поиск приемлемого m.
Мне же желательно отыскать универсальный принцип
задания этого параметра, чтобы без труда получалось решение для сколь угодно
большой матрицы n x
n . На этом этапе возникает потребность разрешить уже чисто философский вопрос: какое
именно нечетное число m лучше всего
характеризует порядок n
= 4k + 2 ? Постановка этого ключевого вопроса создает в
голове вспышку озарения и обеспечивает ясное видение цели.
Конечно же:
m = n/2 = 2k +
1 !!!
Итак, золотую рыбку я поймал. Теперь остается
технически грамотно распорядиться ценной добычей.
Возвращаюсь к полустолбцам. На Рис. 5 показаны два возможных начала:
a) b)
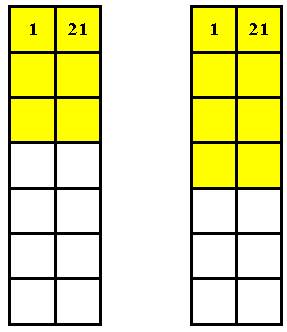
Рис. 5.
Число
справа от единицы получаю
элементарно: n + n/2 .
При n = 14 это
21. Мне теперь известна постоянная S = 1,5 n +
1 = 22. Достаточно выявить по одному числу в каждой строке, чтобы найти его
дополнение.
Теперь думаю: зачем под единицей помещать какое-то
несоразмерно большое число? Раз нужно писать только нечетный ряд, то естественней всего задать его регулярным,
то есть в виде арифметической прогрессии. Создаю предельно простые схемы (Рис.
6):
a) b)
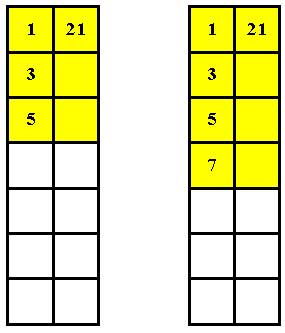
Рис. 6.
Только как быть с четными числами? Самое логичное было бы, чтобы весь левый
ряд шел по нарастающей, то есть не имел бы “дерганных
точек”. Но с чего начать? Рассуждаю так: пусть в нижней левой ячейке будет
стоять число, на единицу меньшее, чем 21 (Рис. 7):
a) b)
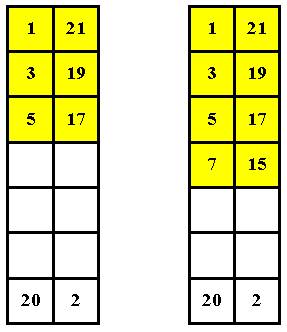
Рис. 7.
Логика тут простая – тогда правый
полустолбец снизу-вверх будет
заполняться последовательным рядом
четных чисел, начиная с 2-х. Сохраняю ранее
принятую тенденцию и окончательно записываю (Рис. 8):
a) b)
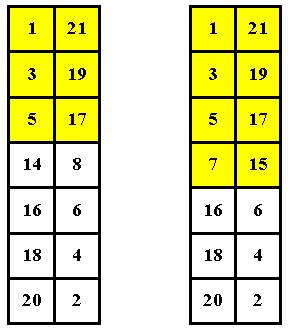
Рис. 8.
Замечаю, что в варианте на Рис.
Но ведь это как раз порядок матрицы n
!!!
Я уже почти уверен, что именно два левых полустолбца
приведут к успеху”.
Быстро составляю программу на языке Yabasic:
rem ПОСТРОЕНИЕ
НЕТРАДИЦИОННОГО ИДЕАЛЬНОГО МК ПОРЯДКА 4k+2
open
#2,"530_G.txt","w":nn=1530:nn2=2*nn
dim
z1(nn,nn),z2(nn,nn2),z(nn,nn),a(nn/2),c(900000)
n=530:k=n/2:k1=(n-2)/4:x=(n+k+1)/2:n1=n+k:s=n1+1:m=n/2*(n1^2+1)
for i=1 to k1:a(i)=2*i-1:next i:for i=1 to
k1+1:a(n/2-i+1)=n1-1-2*(i-1):next i:for i=1 to n/2:z1(i,1)=a(i):next i
for i=n/2+1 to n:z1(i,1)=z1(n-i+1,1):next i
for i=1 to n:z1(i,2)=s-z1(i,1):next i:for
k0=1 to n/2-1
for i=1 to n:z1(i,2*k0+1)=z1(i,1):z1(i,2*k0+2)=z1(i,2):next i
next
k0:u=0:for i=1 to n:for j=1
to n:z(i,j)=n1*(z1(i,j)-1)+z1(j,i):next j:next i:s0=0:for i=1 to
n:s0=0:for j=1 to n:s0=s0+z(i,j):next j:if s0=m then u=u+1:fi:next i:s0=0:for j=1 to n:s0=0:for i=1 to n:s0=s0+z(i,j):next i:if s0=m then u=u+1:fi:next j:for
i=1 to n:for j=n+1 to n+n:z(i,j)=z(i,j-n):next
j:next i:s0=0:for j=1 to n:s0=0:for i=1 to n:s0=s0+z(i,i+j-1):next i:if
s0=m then u=u+1:fi:next j:s0=0:for j=1 to n:s0=0:for i=n
to 1 step -1:s0=s0+z(i,i+j-1):next i:if s0=m then
u=u+1:fi:next j
if
u=4*n then:for i=1 to n*n:c(i)=0:next i:for
i= 1 to n:for j=1 to n:z=z(i,j):c(z)=c(z)+1:next j:next i:c=0:for i=1 to n*n:if c(i)>1 then c=c+1:fi:next i:if
c=0 then:for i=1 to
n/2:print #2,a(i);:next i:print
#2," ";:print #2,k1,x,k:for i=1 to n/2:print a(i);:next i:print:for i=1 to n:for j=1 to n:print #2,z(i,j);:next j:print #2:next i:print #2:print #2:fi:fi
Здесь производится проверка на пандиагональность и на
отсутствие дублирования чисел. Мои ожидания полностью оправдались: по
единому принципу находятся все идеальные нетрадиционные магические квадраты
порядка 4k + 2. Общая схема составления двух полустолбцов следующая
(Рис. 9):
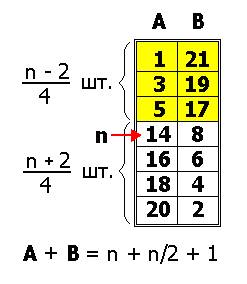
Рис. 9.
Универсальный способ построения двух полустолбцов,
предложенный Г.Александровым.
Даже
и не знаю – можно ли изобрести более простую цепь чисел?
Характерные точки: 5 ----> (n – 4)/2 ; 20 ----> 1,5 n – 1 ;
17 ----> n + 3 ; 8 ---->
(n + 2)/2 .
Латинский квадрат в этом случае такой (Рис. 10):
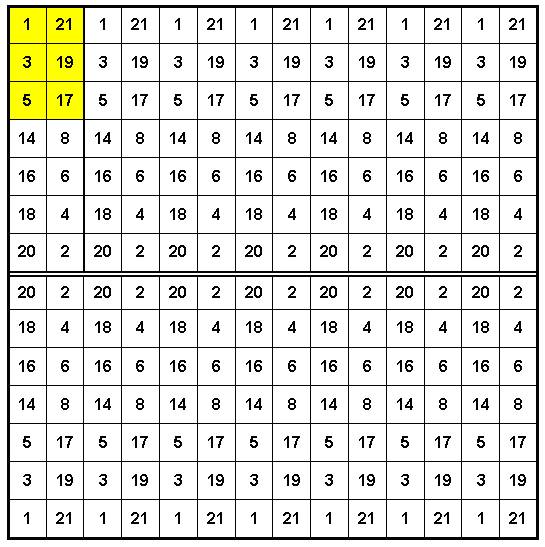
Рис. 10. Латинский квадрат Г.Александрова при n = 14
Окончательное решение для n = 14 (Рис. 11):
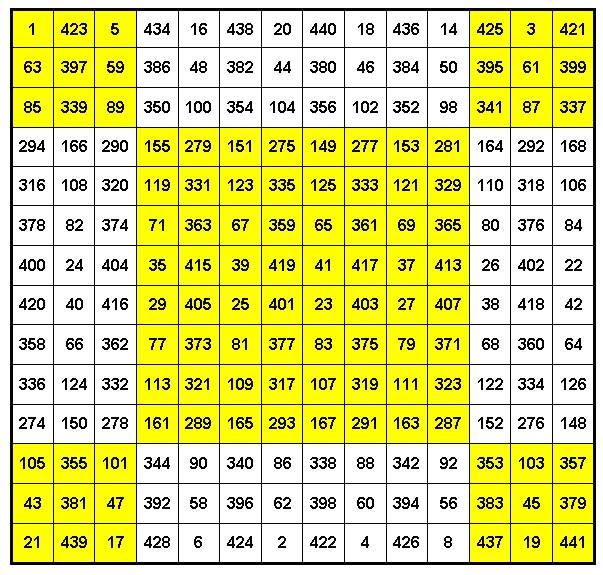
Рис. 11. Идеальный нетрадиционный
совершенный магический квадрат Г.Александрова 14 х 14
Следует заметить, что пары
чисел в строках (Рис. 9 ) можно как угодно менять местами. В результате все равно будут
получаться идеальные нетрадиционные магические квадраты.
2.
Идеальные совершенные магические
квадраты
порядка 8k и 8k + 4
Описанный выше метод
построения латинских квадратов можно использовать и для всех остальных четных
порядков n , то есть для n =
8k и n = 8k +
4. Различия – только в наборе чисел в
двух полустолбцах. Здесь параметр m = 0 и, следовательно,
магические квадраты являются традиционными.
Вот как мне удалось
решить эту задачу.
Поскольку m=0, то в двух
полустолбцах должны быть задействованы все числа от 1 до n. Так
как n – число четное, то обязательно присутствуют n/2 нечетных чисел и столько же четных. Создадим пробные регулярные схемы, например,
такие (Рис. 12):
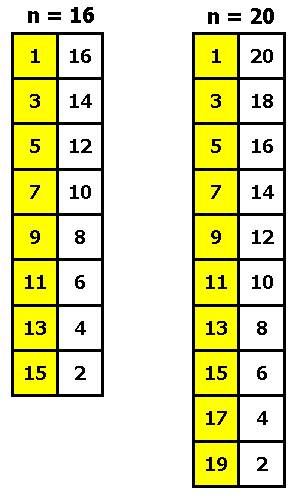
Рис. 12. Регулярное заполнение числами полустолбцов
У меня была слабая
надежда, что решение сразу получится. Однако, чудес в
сложных задачах не бывает. Тогда пришла в голову мысль: буду менять местами нечетные
и соответствующие им четные дополнения. Использовал для этой цели метод
Монте-Карло. То есть случайным образом задавал как количество пар чисел,
которые нужно обменять, так и места их расположения (т.е. номера строк). К
счастью, на мониторе стали появляться долгожданные
цепочки чисел, характеризующие идеальные совершенные магические квадраты.
Просмотрев все варианты и проанализировав их для разных значений n
, мне
удалось найти две общие схемы построения полустолбцов (Рис. 13):
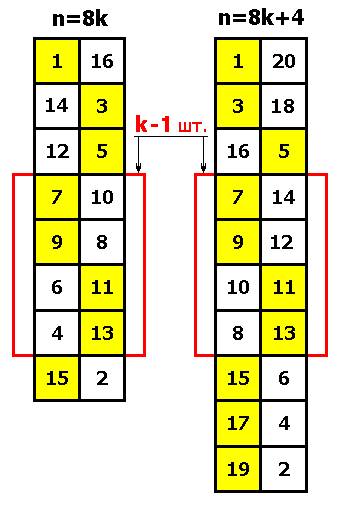
Рис. 13 Универсальные способы построения двух
полустолбцов,
Блок в красной рамке
повторяется k - 1 раз один за другим. Видно,
что регулярность четных и нечетных чисел сохранилась – просто они стали
располагаться не строго вертикально, а “змейками“.
Эти две модели справедливы для любого k
, начиная с
единицы. Опять же, пары чисел потом можно как угодно менять в полустолбце – все
равно получится идеальный совершенный магический квадрат.
Покажу готовые
квадраты для приведенных выше вариантов (Рис. 14 и 15) :
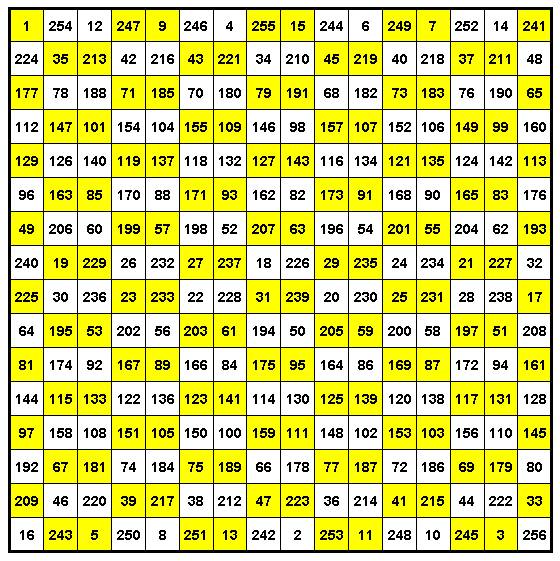
Рис. 14. Идеальный совершенный магический квадрат 16 х 16
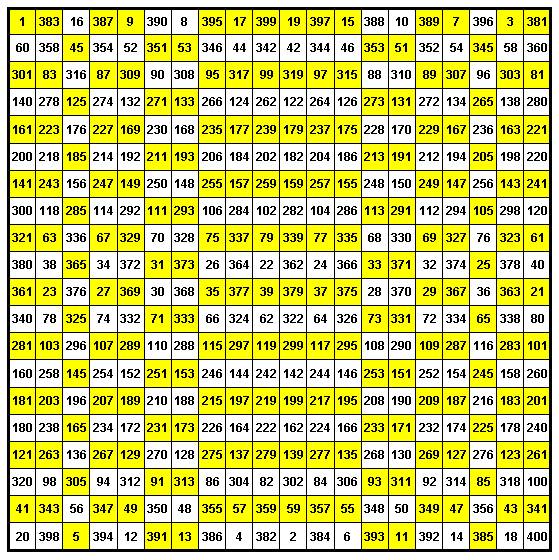
Рис. 15. Идеальный совершенный магический квадрат 20 х 20
Высшая истина рождается в споре с собой.
14 ноября –
4 декабря
Сидней