Георгий Александров

Число π ,

число e …

В этой статье я не буду касаться вопроса истории величайших математических констант, не буду говорить о захватывающей гонке за точность их вычислений, о рекордах и бесконечных числовых рядах. Обо всем этом можно прочитать на многочисленных страницах Интернета. Здесь же – итог поисков компактных формул, с помощью которых удается получать свыше шести верных значащих чисел для приближенных значений π и e .

В 1914 году великий индийский математик С. Рамануджан вывел необычайно эффективный ряд для быстрого вычисления числа π с очень большой точностью (http://mathworld.wolfram.com/PiFormulas.html):

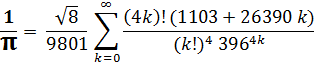
Если перевернуть дробь, то в системе Maple будем иметь:

P := 9801/4*2^(1/2)/Sum((4*k)!*(1103+26390*k)/k!^4/(396^(4*k)),k = 0 .. m);

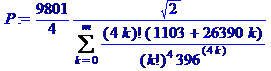
При m = 0:

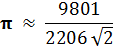
В этой формуле ошибка от точного значения константы составляет . Число верных значащих цифр t = 7 , а число цифр в формуле n = 9 .

При m = 1:

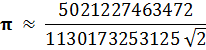
Ошибка , t = 16 , n = 27 .

При m = 2:

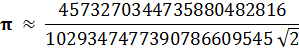
Ошибка , t = 24 , n = 45 .

В общем случае t = 8(m+1) ; n = 18m + 9

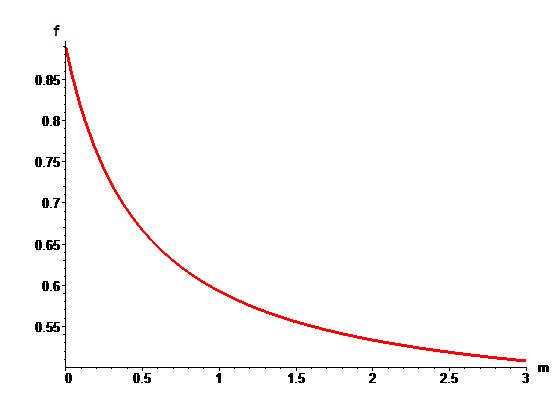
Отношение

всегда меньше единицы. То есть число цифр в приближенных формулах меньше числа верных значащих цифр константы (см. Рис.):

Моя цель – найти приближенные формулы, в которых t - не меньше, чем n. Достичь такой цели удалось при помощи несложной комбинаторной программы. Один из блоков ее на языке “Yabasic” выглядит так:

open #1,"Pi_E.txt","w"

e0=2.7182818284590452354:p0=3.1415926535897932385:v=99

for a1=1 to v :for a2=a1 to v : for a3=a2 to v : for a4=a3 to v

for n1=-1 to 1 step 2: for m1=1 to 3: for n2=-1 to 1 step 2

for m2=1 to 3: for n3=-1 to 1 step 2: for m3=1 to 3

for n4=-1 to 1 step 2: for m4=1 to 3

d=a1^(n1/m1)*a2^(n2/m2)*a3^(n3/m3)*a4^(n4/m4)

if abs(d-e0)<10^(-6) then print "NUMBER E ";:print a1,n1,m1,a2,n2,m2,a3,n3,m3,a4,n4,m4,d-e0

print #1, "NUMBER E ";:print #1,a1,n1,m1,a2,n2,m2,a3,n3,m3,a4,n4,m4,d-e0:fi

if abs(d-p0)<10^(-6) then print "NUMBER PI ";:print a1,n1,m1,a2,n2,m2,a3,n3,m3,a4,n4,m4,d-p0

print #1,"NUMBER PI ";:print #1, a1,n1,m1,a2,n2,m2,a3,n3,m3,a4,n4,m4,d-p0:fi

next m4:next n4:next m3:next n3:next m2:next n2:next m1:next n1

next a4:next a3:next a2:next a1

По этой программе были найдены формулы 1) и 2) (см. ниже). Остальные выражения получены по несколько видоизмененной программе.

1) ; ошибка ; t = 7 ; n = 6 ; f = 1,167

2) ; ошибка ; t = 7 ; n = 7 ; f = 1

3) ; ошибка ; t = 9 ; n = 7 ; f = 1,286

4) ; ошибка ; t = 10 ; n = 8 ; f = 1,25

5) ; ошибка ; t = 9 ; n = 9 ; f = 1

6) ; ошибка 1 ; t = 8 ; n = 7 ; f = 1,143

Последние шесть формул являются доказательством беспредельной гибкости иррациональных чисел. С их помощью можно точно и сжато производить аппроксимацию любых теоретических и эмпирических констант.

Самыми примечательными, на мой взгляд, являются формулы 3) и 4), поскольку у них наблюдаются экстремально высокие параметры t и f .

Более лучшие приближения удалось найти для e :

7) ошибка ; t =8 ; n =8 ; f = 1