Георгий Александров
Красивый способ построения
магических квадратов
Находить новые магические квадраты (или МК) – это истинное наслаждение для любителя
головоломок. Еще интересней выявлять простые методы составления волшебных
матриц. Но самое прекрасное – обнаружить элементарный единый подход к созданию
абсолютно всех магических квадратов.
Кажется, мне это удалось путем использования
латинских квадратов. Универсальный способ построения МК можно условно назвать “методом
цифровых волн”. Рассмотрим его применительно к трем группам магических
квадратов:
- нечетного порядка ;
- порядка двойной четности ;
- порядка одинарной четности.
1.
Магические квадраты порядка n = 2k + 1
Латинский квадрат можно построить по следующему
принципу. Пусть “цифровой ветер“ дует в направлении желтой стрелки, то есть
справа налево и вниз (это направление совпадает с главной диагональю квадрата).
Тогда будет образовываться линейный фронт цифровой волны, причем единичная
волна находится на пересечении со средней ячейкой самой верхней строки матрицы
(желтый ряд на Рис. 1):
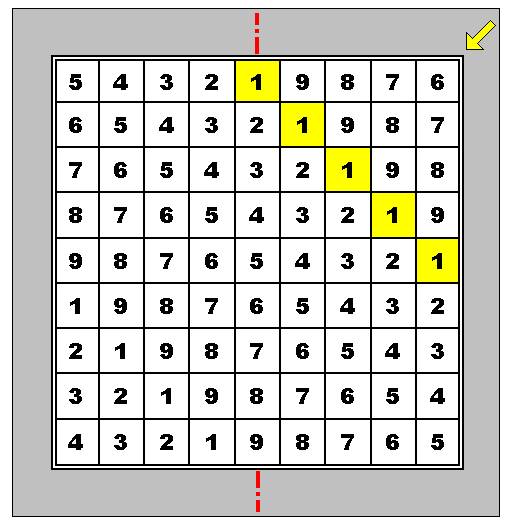
Рис. 1. Одиночная
цифровая волна
Вот и вся подготовительная работа.
Пусть числа в ячейках данной матрицы – это Z( i, j ) , а Zmax – наибольшее число в
поле латинского квадрата. Тогда магический квадрат M(i,j) строится согласно правилу:
M(
i,j ) = Zmax [Z(
i , j ) –
1 ] +
Z( i , n+1 - j)
Допустим, начало координат находится в левом верхнем углу. Параметр i – номер строки , j – номер столбца. В нашем примере Zmax = 9. При i =2 j = 3 Z( 2 , 3 ) = 4 ; Z( 2 , 9+1-3) =Z(2,7) = 9. Следовательно, M( 2 , 3 ) = 9 ( 4 – 1 ) + 9 = 36 . Вычислив таким образом все M( i,j ), получим решение (Рис. 2):
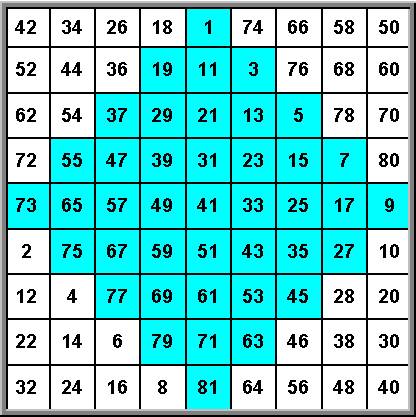
Рис. 2.
Магический квадрат 9 х 9
В данном решении имеет место компактное ядро
нечетных чисел (цветная область)
2.
Магические квадраты порядка n = 4k
Для построения
латинского квадрата потребуется уже два горизонтальных цифровых ветра: один “дует”
слева направо (для желтой области ячеек), другой – справа налево (для белых
ячеек). На Рис. 3 показан принцип образования цифровых волн:
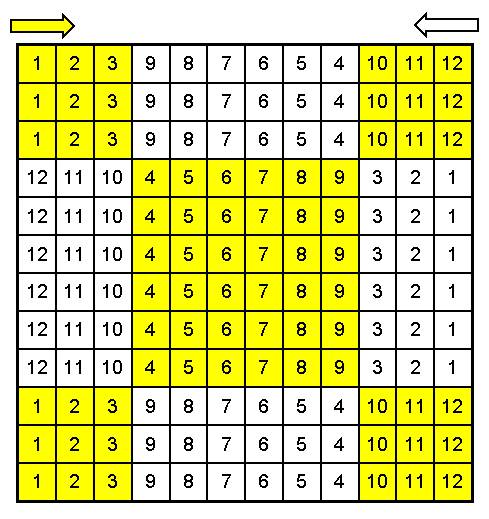
Рис. 3. Система двух
цифровых волн
Пусть числа в ячейках латинского квадрата – это Z( i, j
) , а Zmax – наибольшее. Тогда
магический квадрат M(i,j) строится согласно правилу:
M( i,j ) = Zmax [Z( i, j ) – 1 ] + Z( j, i)
Допустим, начало координат находится в левом верхнем углу. Параметр i – номер строки , j – номер столбца. В нашем примере Zmax = 12. При i =2 j = 3 Z( 2 , 3 ) = 3 ; Z( 3 , 2) = 2. Следовательно, M( 2 , 3 ) = 12 ( 3 – 1 ) + 2 = 26 . Вычислив таким образом все M( i,j ), получим решение (Рис. 4):
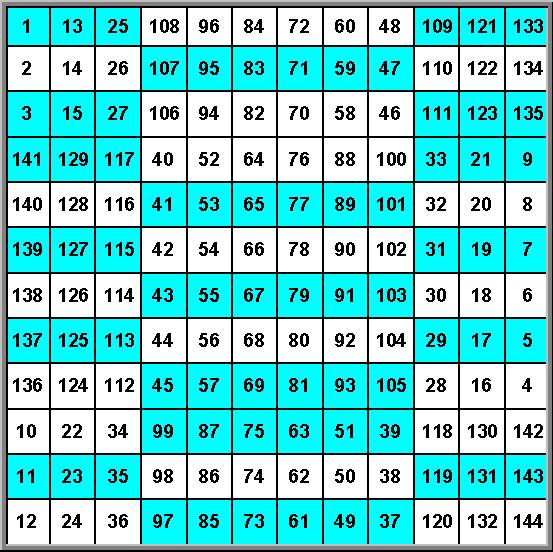
Рис. 4. Магический
квадрат 12 х 12
Нечетные числа расположены симметрично
относительно средней вертикали.
3.
Магические квадраты порядка n = 4k + 2
Теперь рассмотрим матрицы 6 х
6, 10 х 10 ,
14 х 14 и так
далее. Каждый, кто составлял магические квадраты данного вида, непременно
сталкивался с более значительными трудностями, нежели при построении МК
нечетного порядка или порядка двойной четности. Тем не менее, мне удалось
разработать общий и достаточно простой способ компоновки этой группы строптивых
головоломок. Он базируется на методе обратимых квадратов, но доведен до
зеркального блеска простоты. Рассмотрим конкретный пример. Пусть n =
4k + 2 = 14 .
Отсюда k = 3 . На Рис. 5 показан
принцип создания обобщенного латинского квадрата:
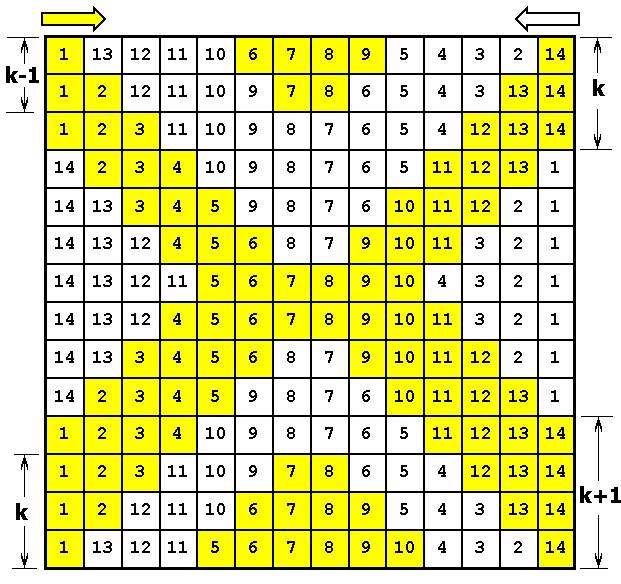
Рис. 5. Построение
обобщенного латинского квадрата 14 х 14
Числа здесь идут двумя регулярными
фронтами с обеих сторон. Вся хитрость заключается в построении желтой области,
параметры которой четко привязаны к величине
k > 0 . Получаем
сразу обобщенный латинский квадрат (или ОЛК).
Теперь
уже можно приступать к созданию магического квадрата.
Пусть числа в ячейках ОЛК – это
Z( i,
j ) , а Zmax – наибольшее число в поле латинского
квадрата. Тогда магический квадрат M(i,j) строится согласно правилу:
M(
i,j ) = Zmax [Z(
i, j ) – 1
] +
Z( j, i)
Допустим, начало координат находится в левом верхнем углу. Параметр i – номер строки , j – номер столбца. В нашем примере Zmax = 14. При i =2 j = 3 Z( 2 , 3 ) = 12 ; Z( 3 , 2) = 2. Следовательно, M( 2 , 3 ) = 14 ( 12 – 1 ) + 2 = 156 . Вычислив таким образом все M( i,j ), получим решение (Рис. 6):
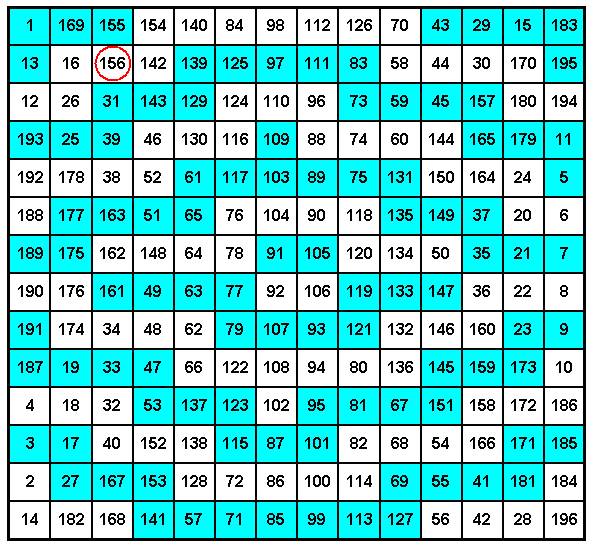
Рис. 6. Магический квадрат 14 х
14
В этом примере выделены
все нечетные числа. Рисунок получился чуть-чуть негармоничным. Отсутствие
полной симметрии подтверждает тезис о сложности рассматриваемой группы
магических квадратов.
Текст программы
для расчета чисел в ячейках МК по найденному латинскому квадрату такой:
rem Программа построения МК порядка n = 4k + 2
dim z(100,100),z1(100,100),c(10000)
open
#1,"14-n.txt","r"
open
#2,"14ms-n.txt","w"
n=14
for i=1 to n:for j=1 to n:input #1 z1(i,j):next j:next i
for i=1 to n:for j=1 to n:z(i,j)=(z1(i,j)-1)*(n)+z1(j,i)
next j:next i: for i=1
to n*n:c(i)=0:next i
for i= 1 to n:for
j=1 to n:z=z(i,j)
c(z)=c(z)+1: next j:next i:c=0: for i=1 to n*n
if c(i)>1 then c=c+1:fi: next i:if c=0 then
for i=1 to n:for j=1 to n:print #2,z(i,j);:if j<n then print #2,",";:fi:next j:print #2:next i:print #2
s0=0:for i=1 to
n:s0=0:for j=1 to n:s0=s0+z(i,j):next j:print #2,s0;:next i:print #2
s0=0:for j=1 to n:s0=0:for i=1
to n:s0=s0+z(i,j):next i:print
#2,s0;:next j:print #2:print #2
for i=1 to n:for j=n+1 to n+n:z(i,j)=z(i,j-n):next j:next i
print
#2
s0=0:for j=1 to n:s0=0:for i=1
to n:s0=s0+z(i,i+j-1):next i:print #2,s0;:next j:print #2
s0=0:for j=1 to n:s0=0:for i=n
to 1 step -1:s0=s0+z(i,i+j-1):next i:print
#2,s0;:next j:print #2:print #2:fi
По этой программе производится проверка
на отсутствие повторений чисел и на магичность.
10-13 декабря
Сидней